Wednesday, December 25, 2013
Fast-food maps — a network analysis
Season's greetings!
For Christmas last year in this blog we had a Network analysis of McDonald's fast-food, in which I examined the food nutrient content of a well-known fast-food vendor. This year I continue the same theme, but expand it to cover an analysis of the geographical locations of various fast-food chains within the USA.
The US restaurant industry included about 550,000 restaurants in 2012 (SDBCNet). Technically, this food industry distinguishes different types of restaurant. The ones we are interested in here are called "quick service restaurants" (QSR), which includes what are known as fast-food and fast-casual restaurants. These are sometimes also called "limited service restaurants".
There are quite a few QSR companies in the USA, and each of them has quite a few locations. In 2012, there were apparently 313,000 fast-food and fast-casual restaurants (Yahoo Finance blog The Exchange), which is more than 50% of the total restaurants. In 2005, more than two-thirds of the largest 243 cities in the US had more fast-food chains than all other restaurant types combined (Zachary Neal).
The QSRs serve an estimated 50 million Americans daily (The Statistic Brain). Indeed, in a 2011 poll of people in 87 U.S. cities, there were several places where >30% of the people had visited QSRs 20+ times in the previous month (nearly once per day), while in all cities >80% of the people had visited at least once (Sandelman & Associates).
The QSR group reports that the national top 20 fast-food chains for 2012 were as shown in the first graph. This includes both company-owned units as well as franchised locations. Note that McDonald's had 34,480 restaurants in its worldwide system, with 14,157 of those being in the USA (The Exchange).
It is of interest to look at how this pattern has changed through time, and so I have taken the data from the QSR group's reports for 2003 to 2012, inclusive (these are the only ones available online). These data are for the number of locations of each of the top 50 chains each year in terms of dollar income. There are 61 chains that appear in the list for at least one of the years, but only 46 of these appeared often enough in the top 50 to be worth including in the analysis.
For this analysis, we can use a phylogenetic network. As usual, I have used the manhattan distance (on range-standardized data) and a neighbor-net network. The result is shown in the next figure. Fast-food chains that are closely connected in the network are similar to each other based on their restaurant numbers over the past decade, and those that are further apart are progressively more different from each other.
The network forms a simple chain from Subway (the biggest) through to the group of very similar-sized chains at the bottom-left. This indicates that most of the restaurant chains have been fairly consistent in their relative sizes throughout the past decade (ie. the big stayed big and the small stayed small), although some chains have changed size. For example, KFC and Taco Bell have each shrunk by 15% since 2007, while Jack in the Box has expanded by 10%.
However, there is a large reticulation in the network involving Starbucks. This is caused by the fact that Starbucks started the decade as a much smaller chain than both Burger King and Pizza Hut, but it is now much larger than either of them. Similarly, there is another reticulation involving Cold Stone Creamery, which expanded rapidly in 2005 (increasing their number of locations by 50%).
The number of locations does not relate directly to dollar turnover, of course, as Subway has much smaller restaurants than do most of the other chains. In this respect, McDonald's leads the way by a considerable margin, with $35,600,000,000 in system-wide sales in the USA during 2012, versus $12,100,000,000 for Subway. This works out at $2,600,000 and $481,000 per restaurant per year, respectively. Starbucks comes in third, with $10,600,000,000 in 2012 ($1,223,000 per unit).
However, let's stick to the number of units, rather than the dollars, and consider their geographical locations. There are several datasets available on the internet that provide this information for different chains (which you actually could get yourself by visiting the homepage of each chain and asking for the location of each restaurant, one at a time!). If you are prepared to pay some money, then you can have the latest list from AggData; but I am not in that league.
However, apparently the man at the Data Pointed blog is in that league, or was in 2010. His mapped version of the data for McDonald's (only) looks like this next figure (each dot represents one restaurant).
This has led him to contemplate the McFarthest Point, which is the point in the contiguous US states that is furthest from a McDonald's restaurant. He reckons that its map co-ordinates are: +41.94389, –119.54010. He has made an excursion to this spot (along with some fast-food), which you can read about in A Visit To The McFarthest Spot.
In turn, this caused the man at the Consumerist blog to contemplate the equivalent spot for Subway. This is currently estimated to be +42.397327, –117.956840 (Is This the Farthest Away You Can Get From a Subway in the Continental U.S.?).
Returning now to the data sources, you could also look at the data from the Food Environment Atlas (by Vince Breneman and Jessica Todd, of the USDA Economic Research Service). At the time of writing, this contains a Map with Fast-food restaurants / 1000 population for 2009, showing each individual county. This refers to the total number of units, summed across all fast food chains. A similar map is available at Business Insider, aggregated by state (but based on the 2008 data).
However, I cannot pay for the data, and I want the data separately for the different fast-food chains. That leads me to the Fast Food Maps by Ian Spiro. In 2007, he scraped the data from the web pages of various chains (as I noted above), and has made it available as a web page and an associated datafile.
He has included data for 10 of the fast-food chains, based on those present in the state of California. So, he covers only 8 out of the top 20 national chains: McDonald's, Burger King, Pizza Hut, Wendy's, Taco Bell, KFC, Jack in the Box, and Hardee's. To these, he adds Carl's Jr (mainly on the West Coast of the USA) and In-N-Out Burger (mainly in the South-West), which I did not include in my analysis.
To analyze these data, I took the information for each chain in each state and divided this by the number of people in that state (to yield the number of restaurants per 100,000 people per chain per state). I then produced a phylogenetic network, as described above, and as shown in the next graph. States that are closely connected in the network are similar to each other based on the density of restaurants of each chain, and those that are further apart are progressively more different from each other. I have color-coded the states to highlight the similarities.
In the network, the states turn out to be arranged roughly geographically, with a few exceptions. In other words, neighboring states have similar densities of restaurants from certain fast-food chains.
For example, the red-colored states are from the West (including in the Pacific!), and they don't have Hardee's, but do have most of the Jack in the Box restaurants. The brown-colored states are from the North Centre, and these have the highest density of Burger King and Pizza Hut. Montana is separate from this grouping because it has a lower density of both Burger King and KFC.
The orange-colored states are from the Mid West and the South, and these have the highest density of Hardee's. Georgia is separate from this grouping because it has a lower density of Hardee's; and Florida is separate because it has a lower density of most chains. The blue-colored states are also from the Mid West, and these have the highest density of McDonald's and Wendy's. Illinois is separate because of a lower density of most chains (particularly KFC) except for McDonald's.
The dark-green-colored states are from the North East, and these don't have Hardee's, and they have the lowest density of Pizza Hut. The light-green-colored states are also from the North East, and these form a separate grouping because they have a higher density of most chains except McDonald's. Maryland is separate because it has an even higher density of most chains (particularly Hardee's); and Delaware has a higher density of Hardee's and Taco Bell.
Finally, Oklahoma and New Mexico have the highest density of KFC.
NB. For an interactive map showing the locations of the 507 Dunkin' Donuts, 269 Starbucks and 235 McDonald's in New York City (in October 2013), check out Mapping the Big Apple's Big Macs, Coffee, and Donuts. The concentration of Starbucks in downtown and midtown Manhattan is truly impressive. Indeed, 43% of the city's cafés are either Dunkin' Donuts or Starbucks (Coffee and Tea in New York City).
Conclusion
So, there you have it — fast-food is not randomly distributed in the USA. Where you live determines how much you have available of the different types. Indeed, as Pam Allison's Blog notes: "Although restaurants like McDonalds are very popular nationwide, they aren’t necessarily the most popular on a local level. In fact, there are only a handful of zip codes in the United States where McDonald's is the most popular. Rather, many local or regional chains are the more likely choice with consumers."
There are many other aspects to the geography of food, especially fast-food; but these can wait until a later blog post.
Labels:
EDA,
Fast food,
Splits graph
Thursday, December 19, 2013
Is rate variation among lineages actually due to reticulation?
Non-congruence among characters has traditionally been attributed solely to so-called vertical evolutionary processes (parent to offspring), which can be represented in a phylogenetic tree. For example, phenotypic incongruence was originally attributed solely to homoplasy (convergence, parallelism, reversal). For molecular data this could be modeled with DNA substitutions and indels, along with allowance for variable rates in different genic regions (e.g. invariant sites, or the well-known gamma model of rate variation).
This approach was not all that successful, and so the substitution models were made more complex, by allowing different evolutionary rates in different branches of the tree (e.g. substitutions are more or less common in some parts of the tree compared to others). For many researchers this is still as sophisticated as their phylogenetic models get (Schwartz & Mueller 2010), allowing for a relaxed molecular clock in their model rather than imposing a strict clock.
There is, however, a fundamental limitation to trying to make any one model more sophisticated: the more complex model will probably fit the data better but it might be fitting details rather than the main picture. Consider the illustration below. There is a lot of variation among these six animals and yet they are all basically the same. If I wish to devise a model to describe them, do I need a sophisticated model that describes all the nuances of their shape variation, or do I need a simple model that recognizes that they are all five-pointed stars? The answer depends on my purpose — if I wish to identify them to class then it is the latter, if I wish to identify them to species then it might be the former.
Vertical process models
This is relevant to phylogenetics. For example, if I wish to estimate a species tree from a set of gene trees, do I need a complex model that deals with all of the evolutionary nuances of the individual gene trees, or a simpler model that ignores the details and instead estimates what the trees have in common? It has been argued that the latter will be more useful under these circumstances. On the other hand, if I am studying gene evolution itself, I may be better off with the former.
So, adding things like rate variation among lineages (and also rate variation along genes) will usually produce "better fitting" models. However, this is fit to the data, and the fit between data and model is not the important issue, because this increases precision but does not necessarily increase accuracy.
Therefore, modern interest is in changing the fundamentals of the model, rather than changing its details. There are many possible causes of gene-tree incongruence, and maybe these should be in the model in order to increase accuracy.
For example, there has been interest in adding other vertical processes to the tree-building model, most notably incomplete lineage sorting (ILS) and gene duplication-loss (DL). ILS means that gene trees are not expected to exactly match the species tree, but will vary stochastically around that tree, with probabilities that can be calculated using the coalescent. DL means that gene copies appear and disappear during evolution, so that gene sequence variation is due to hidden paralogy as well as to orthology.
ILS has been modeled by being integrated into a more sophisticated DNA substitution model (see the papers in Knowles & Kubatko 2010). Originally, DL was dealt with at the whole-gene level (Slowinski and Page 1999; Ma et al. 2000), but there have been recent attempts to integrate this into the DNA substitution models, as well (Åkerborg et al. 2009; Rasmussen & Kellis 2012). These models are not yet widely used, and so most published empirical species trees still rely on modeling incongruence using rate variation among branches.
Horizontal process models
However, this whole approach restricts the phylogenetic model to vertical processes alone. It is entirely possible that the sequence variation that is being attributed to rate variation among branches is actually being caused by horizontal evolutionary processes, such as recombination, hybridization, introgression or horizontal gene transfer (HGT). For example, an influx of genetic material from outside a lineage could be mis-interpreted as an increase in the rate of substitutions and indels within that lineage. That is, long branches might represent introgression (or HGT) rather than in situ rate variation. If this is true then we would be modeling the wrong thing.
There has been little explicit discussion of this point in the literature. Syvanen (1987) seems to have been among the first. However, his premise was that the molecular clock is ultimately correct (and that "the basic observation has been that different macromolecules yield roughly the same phylogenetic picture"), and he was arguing that HGT does not necessarily violate the clock. Our modern perspective is, of course, that a strict clock is unlikely unless it has been demonstrated, and that genes are incongruent as often as they are congruent.
Recent models for ILS and DL have started to broach this issue, by adding reticulation to their underlying models. Rather oddly, this has usually been described as:
- ILS + hybridization (Meng & Kubatko 2009; Kubatko 2009; Joly et al. 2009; Bloomquist & Suchard 2010; Yu et al. 2011; Marcussen et al. 2012; Jones et al. 2013; Yu et al. 2013); and
- DL + HGT (Mirkin et al. 2003; Górecki 2004; Hallett et al. 2004; Csürös & Miklós 2006; Doyon et al. 2010; Tofigh et al. 2011; Bansal et al. 2012; Sjöstrand et al. 2012).
Conclusion
The point here is essentially the same one that I made in a previous post (Resistance to network thinking). Currently, phylogenetics is approached in a very conservative manner. The "old way" is the best way, and things change very slowly. The currently popular phylogenetic models are simply variants of the same models that have been used for 30 years. Temporal rate variation (among lineages) and spatial rate variation (along genes) have been added to the original model from the 1970s, but not yet more complex vertical processes (ILS or DL), and not yet horizontal processes. For these, specialist programs need to be used.
Essentially, all variation in branch length is still attributed to homoplasy and rate variation, rather than considering the myriad of other biological processes that will produce the same apparent phenomen. With this attitude we might be getting more precise models but not necessarily more accurate one.
References
Åkerborg Ö, Sennblad B, Arvestad L, Lagergren J (2009) Simultaneous bayesian gene tree reconstruction and reconciliation analysis. Proceedings of the National Academy of Sciences of the USA 106: 5714-5719.
Bansal MS, Alm EJ, Kellis M (2012) Efficient algorithms for the reconciliation problem with gene duplication, horizontal transfer and loss. Bioinformatics 28: i283-i291.
Bloomquist EW, Suchard MA (2012) Unifying vertical and nonvertical evolution: a stochastic ARG-based framework. Systematic Biology 59: 27-41.
Csürös M, Miklós I (2006) A probabilistic model for gene content evolution with duplication, loss, and horizontal transfer. Lecture Notes in Computer Science 3909: 206-220.
Doyon J-P, Scornavacca C, Gorbunov KY, Szöllösi GJ, Ranwez V, Berry V (2019) An efficient algorithm for gene/species trees parsimonious reconciliation with losses, duplications and transfers. Lecture Notes in Computer Science 6398: 93-108.
Górecki P (2004) Reconciliation problems for duplication, loss and horizontal gene transfer. In: Bourne PE, Gusfield D (editors). Proceedings of the 8th Annual International Conference on Research in Computational Molecular Biology, pp. 316-325. ACM Press, New York.
Hallett M, Lagergren J, Tofigh A (2004) Simultaneous identification of duplications and lateral transfers. In: Bourne PE, Gusfield D (editors). Proceedings of the 8th Annual International Conference on Research in Computational Molecular Biology, pp. 347-356. ACM Press, New York.
Joly S, McLenachan PA, Lockhart PJ (2009) A statistical approach for distinguishing hybridization and incomplete lineage sorting. American Naturalist 174: E54-E70.
Jones G, Sagitov S, Oxelman B (2013) Statistical inference of allopolyploid species networks in the presence of incomplete lineage sorting. Systematic Biology 62: 467-478.
Knowles LL, Kubatko LS (editors) (2010) Estimating Species Trees: Practical and Theoretical Aspects. Wiley-Blackwell, Hoboken NJ.
Kubatko L (2009) Identifying hybridization events in the presence of coalescence via model selection. Systematic Biology 58: 478-488.
Ma B, Li M, Zhang L (2000) From gene trees to species trees. SIAM Journal on Computing 30:
729-752.
Marcussen T, Jakobsen KS, Danihelka J, Ballard HE, Blaxland K, Brysting AK, Oxelman B (2012) Inferring species networks from gene trees in high-polyploid North American and Hawaiian violets (Viola, Violaceae). Systematic Biology 61: 107-126.
Meng C, Kubatko LS (2009) Detecting hybrid speciation in the presence of incomplete lineage sorting using gene tree incongruence: a model. Theoretical Population Biology 75: 35-45.
Mirkin BG, Fenner TI, Galperin MY, Koonin EV (2003) Algorithms for computing parsimonious evolutionary scenarios for genome evolution, the last universal common ancestor and dominance of horizontal gene transfer in the evolution of prokaryotes. BMC Evolutionary Biology 3: 2.
Rasmussen MD, Kellis M (2012) Unified modeling of gene duplication, loss, and coalescence using a locus tree. Genome Research 22: 755-765.
Schwartz RS, Mueller RL (2010) Variation in DNA substitution rates among lineages erroneously inferred from simulated clock-like data. PLoS One 5: e9649.
Sjöstrand J, Sennblad B, Arvestad L, Lagergren J (2012) DLRS: gene tree evolution in light of a species tree. Bioinformatics 28: 2994-2995.
Slowinski J, Page RDM (1999) How should species phylogenies be inferred from sequence
data? Systematic Biology 48: 814-825.
Syvanen M (1987) Molecular clocks and evolutionary relationships: possible distortions due to horizontal gene flow. Journal of Molecular Evolution 26: 16-23.
Tofigh A, Hallett M, Lagergren J (2011) Simultaneous identification of duplications and lateral gene transfers. IEEE/ACM Transactions on Computational Biology and Bioinformatics 8: 517-535.
Yu Y, Barnett RM, Nakhleh L (2013) Parsimonious inference of hybridization in the presence of incomplete lineage sorting. Systematic Biology 62: 738-751.
Yu Y, Than C, Degnan JH, Nakhleh L (2011) Coalescent histories on phylogenetic networks and detection of hybridization despite incomplete lineage sorting. Systematic Biology 60: 138-149.
Labels:
Philosophy,
Phylogeny
Monday, December 16, 2013
Phylogenetics, ecologist style
Many of us are familiar with how a phylogeneticist, systematist or evolutionary biologist constructs a phylogenetic tree. However, ecologists apparently do it differently. Scott Chamberlain explains this procedure in one of his blog posts (Networks phylogeny):
There were about 500 species to make a phylogeny for, including birds and insects, and many species that were bound to end up as large polytomies. I couldn't in reasonable time make a molecular phylogeny for this group of species, so I made one ecologist style.
That is, I:He then describes this process in more detail, which he hopes "makes it more reproducible". Here is his final tree (produced by FigTree).
Unfortunately, this process can't all be collected in an R script.
- Created a topology using Mesquite software from published phylogenies, then
- Got node age estimates from timetree.org (p.s. Wish I could use the new datelife.org, but there isn't much there quite yet), then
- Used the bladj function in Phylocom to stretch out the branch lengths based on the node estimates.
This is an interesting bioinformatic solution to a biological problem, when empirical data collection has failed. I am not sure that I can recommend its widespread use, though.
Thursday, December 12, 2013
Textbooks and phylogenetic networks
The question has been asked as to which of the current general books about phylogenetics actually cover phylogenetic networks. There are collections of essays where networks are covered, and there are specialist books, of course, but the question here is about general introductory books. While a number of books mention tree incongruence, and that this phenomenon could be represented using a reticulating graph, there appear to be only two books that specifically cover the topic of phylogenetic networks.
(1)
Barry G. Hall (2011) Phylogenetic Trees Made Easy: A How-To Manual, Fourth Edition. Sinauer Associates, Sunderland MA.
The first three editions (2001, 2004, 2008) discussed trees only, but the fourth edition has added a chapter on networks. Chapter 15 (pp. 219-248) explicitly notes that "The material presented here is drawn almost entirely from the new book Phylogenetic Networks: Concepts Algorithms and Applications", which is also noted was "made available to me in manuscript prior to its publication."
There are four sections in the chapter:
Why Trees Are Not Always Sufficient
Unrooted and Rooted Phylogenetic Networks
Learn More about Phylogenetic Networks
Using SplitsTree to Estimate Unrooted Phylogenetic Networks
Using Dendroscope to Estimate Rooted Networks from Rooted Tree
The first three sections are theoretical introductions to the topic, and the final two sections proceed through a worked example (a different one each).
The book provides a basic introduction to phylogenetics, which is its intent. So, the network topics are presented in a straightforward manner, which makes them easy to grasp. The worked examples are cookbook style, intended solely to get you started using the two chosen computer programs.
The author is to be congratulated for producing not only the first, but so far the only, general book that covers evolutionary networks.
(2)
Philippe Lemey, Marco Salemi, Anne-Mieke Vandamme (editors) (2009) The Phylogenetic Handbook: A Practical Approach to Phylogenetic Analysis and Hypothesis Testing, Second Edition. Cambridge Uni Press, Cambridge.
The first edition (2003) had a chapter on SplitsTree by Vincent Moulton, and this was revised in the current edition to Split Networks: a Tool for Exploring Complex Evolutionary Relationships in Molecular Data, Chapter 21 (pp. 631-653), by Vincent Moulton and Katharina Huber.
The chapter provides a general introduction to the theory of splits graphs and their uses; and the practical exercises use SplitsTree. This was the first general book on phylogenetics to include networks, although evolutionary networks are not covered.
Conclusion
The coverage of networks is the final topic in the book in both cases, so it can hardly be claimed to have an important place. Nevertheless, these books are at least one step ahead of their competitors.
All of these books are examples of the contemporary focus on congruent tree patterns in evolution, with reticulate relationships being almost an afterthought. There is nothing in the word "phylogeny" that specifies a shape for evolutionary history — it comes from the Greek phylon "race" + geneia "origin". Evolutionary groups may arise by either vertical or horizontal processes, and so evolution may be tree-like or it may not. The current focus almost exclusively on trees is therefore somewhat misplaced.
Labels:
Books,
Dendroscope,
Evolutionary network,
Splits graph
Monday, December 9, 2013
Results of some bioinformatics polls
In 2008, Michael Barton conducted a Bioinformatics Career Survey. Since then, various groups have updated some of that information by conducting polls of their own. Below, I have included some of the more recent results, for your edification.
This first one comes from the Bioinformatics Organization, in response to the question: What is your undergraduate degree in? It is interesting to note that more bioinformaticians are biologists by training, rather than computational people.
The next one is actually an ongoing poll at BioCode's Notes, in response to the question: Which are the best programming languages for a bioinformatician? R is an interesting choice as the most useful language, given the more "traditional" use of Perl and Python.
That leads logically to another of the Bioinformatics Organization's questions: Which computer language are you most interested in learning (next) for bioinformatics R&D? I guess that if you already know R, then either Python or Perl is a useful thing to learn next.
Furthermore, the Bioinformatics Organization also asked: Which math / statistics language / application do you most frequently use? The choice of R here is more obvious, given that it is free, which most of the others are not. I wonder what the answer "none of the above" refers to.
Labels:
Bioinformatics,
computational biology,
Polls,
software
Wednesday, December 4, 2013
The phylogenetics of Little Red Riding Hood
A couple of weeks ago we received an unexpected influx of visitors to this blog, being directed here by at article at the NBC News site. This article cited one of our blog posts (Network analysis of Genesis 1:3) as an example of the use of phylogenetic analysis in stemmatology (the discipline that attempts to reconstruct the transmission history of a written text). The NBC article itself is about a recently published paper that applies these same techniques to an oral tradition instead — the tale of Little Red Riding Hood. This paper has generated much interest on the internet, being reported in many blog posts, on many news sites, and in many twitter tweets. After all, the young lady in red has been known for centuries throughout the Old World.
Needless to say, I had a look at this paper (Jamshid J. Tehrani. 2013. The phylogeny of Little Red Riding Hood. PLoS One 8: e78871). The author collated data on various characteristics of 58 versions of several folk tales, such as plot elements and physical features of the participants. These tales included Little Red Riding Hood (known as Aarne-Uther-Thompson tale ATU 333), which has long been recorded in European oral traditions, along with variants from other regions, including Africa and East Asia (where it is known as The Tiger Grandmother), as well as another widespread international folk tale The Wolf and the Kids (ATU 123), which has been popular throughout Europe and the Middle East. As the author notes: "since folk tales are mainly transmitted via oral rather than written means, reconstructing their history and development across cultures has proven to be a complex challenge."
He produced phylogenetic trees from both parsimony and bayesian analyses, along with a neighbor-net network. He concluded: "The results demonstrate that ... it is possible to identify ATU 333 and ATU 123 as distinct international types. They further suggest that most of the African tales can be classified as variants of ATU 123, while the East Asian tales probably evolved by blending together elements of both ATU 333 and ATU 123." His network is reproduced here.
There is one major problem with this analysis: all three graphs are unrooted, and you can't determine a history from an unrooted graph. A phylogeny needs a root, in order to determine the time direction of history. Without time, you can't distinguish an ancestor from a descendant — the one becomes the other if the time direction is reversed. Unfortunately, the author makes no reference to a root, at all.
So, his recognition of three main "clusters" in his graphs is unproblematic (ATU 333; East Asian; and ATU 123 + African) although the relationship of these clusters to the "India" sample is not clear (as shown in the network). On the other hand, his conclusions about the relationships among these three groups is not actually justified in the paper itself.
Rooting the trees
So, the thing to do is put a root on each of the graphs. We cannot do this for the network, but we can root the two trees, and we can take the nearest tree to the network and root that, instead.
There are several recognized ways to root a tree in phylogenetics (Huelsenbeck et al. 2002; Boykin et al. 2010):
- a character transformation series (i.e. non-reversible substitution models)
- an outgroup
- mid-point rooting
- assume clock-like character replacement (e.g. the molecular clock).
I therefore did the following:
- For the parsimony analysis, I imported the author's consensus tree into PAUP* (the program he used to produce it), calculated the branch lengths with ACCTRAN optimization, and found the midpoint root.
- For the bayesian analysis, I re-ran the MrBayes analysis exactly as described by the author, except that I added a relaxed clock (with independent gamma rates model for the variation of the clock rate across lineages).
- For the phylogenetic network, the neighbor-net is basically the network equivalent of a neighbor-joining tree, and so I calculated this in SplitsTree (the program the author used), and found the midpoint root.
- Also, the strict clock version of a neighbor-joining tree is a UPGMA tree, which I calculated using SplitsTree.
Having the East Asian samples as the sister to the other tales does not match what would be expected for the historical scenario suggested by the original author from his unrooted graphs — that the East Asian tales "evolved by blending together elements of both ATU 333 and ATU 123".
Instead, this placement exactly matches an alternative theory that the author explicitly rejects: "One intriguing possibility raised in the literature on this topic ... is that the East Asian tales represent a sister lineage that diverged from ATU 333 and ATU 123 before they evolved into two distinct groups. Thus, ... the East Asian tradition represents a crucial 'missing link' between ATU 333 and ATU 123 that has retained features from their original archetype ... Although it is tempting to interpret the results of the analyses in this light, there are several problems with this theory."
The UPGMA root, on the other hand, would be consistent with the blending theory for the origin of the East Asian tales. However, this tree actually presents the African tales as distinct from ATU 123, rather than being a subset of it.
Anyway, the bottom line is that you shouldn't present scenarios without a time direction. History goes from the past towards the present, and you therefore need to know which part of your graph is the oldest part. A family tree isn't a tree unless it has a root.
References
Boykin LM, Kubatko LS, Lowrey TK (2010) Comparison of methods for rooting phylogenetic trees: a case study using Orcuttieae (Poaceae: Chloridoideae). Molecular Phylogenetics & Evolution 54: 687-700.
Huelsenbeck J, Bollback J, Levine A (2002) Inferring the root of a phylogenetic tree. Systematic Biology 51: 32-43.
Labels:
Anthropology,
Directed graph,
Phylogeny,
Rooting,
Stemmatology
Monday, December 2, 2013
The bioRxiv — not just a preprint server for biology
The physical sciences have long had preprint archives, notably the arXiv (founded in 1991), which is managed by Cornell University Library. Bioinformaticians have been active users of these archives, at least partly because getting mathematical papers published can take up to 2 years (see Backlog of mathematics research journals). Bioinformatics moves faster than that. There have been more general preprint services, as well, such as Nature Precedings, which operated from 2007 to 2012.
There have recently been moves afoot to provide similar services specifically for biologists; and the beta version of the bioRxiv has now come online:
bioRxiv (pronounced "bio-archive") is a free online archive and distribution service for unpublished preprints in the life sciences. It is operated by Cold Spring Harbor Laboratory, a not-for-profit research and educational institution. By posting preprints on bioRxiv, authors are able to make their findings immediately available to the scientific community and receive feedback on draft manuscripts before they are submitted to journals.
Many research journals, including all Cold Spring Harbor Laboratory Press titles, EMBO Journal, Nature journals, Science, eLife, and all PLOS journals allow posting on preprint servers such as bioRxiv prior to publication. A few journals will not consider articles that have been posted to preprint servers.Preprint policies are summarized here: List of academic journals by preprint policy.
Many people seem to see archives such as this as having their principal role in bridging the publication delay caused by the peer-review process (see The case for open preprints in biology for a summary of the argument). Indeed, much of the online discussion of preprints in biology seems to be about why biologists have not taken to preprints like ducks to water, asking the rhetorical question: "What are biologists afraid of?" This question pre-supposes that everyone should use preprints unless there is a good reason not to, rather than the more obvious assumption that no-one will use them unless there is a good reason to do so. On the whole, shortening the peer-review process by a few months (as is typical in biology) hardly seems like a sufficient incentive for mass usage of preprints.
However, there does seem to be a possible incentive beyond break-neck speed. An equally important point is that archives act as a powerful means of making unpublished work available online. Even if a particular manuscript is ultimately never published in a journal or book, it will still be available in the archive in its final draft form, since the archives are intended to be permanent repositories. That is, the archives are not only for pre-prints.
There are many reasons why some work never gets formally published, including incompleteness of the data, negative results, lack of perceived profundity, and being out of synch with current trends. If there is nothing inherently faulty about a manuscript, then there is no reason for it to remain unavailable to interested readers. We are no longer beholden to the publishers (or to the referees) for disseminating our data and/or ideas, although we may still prefer formal publication as the primary conduit.
For example, I started using the arXiv after it added a section on "Quantitative Biology" in 2003. I have several manuscripts in the ArXiv that, for one reason or another, have not (yet) made it into print:
- Morrison DA (2005) Counting chickens before they hatch: reciprocal consistency of calibration points for estimating divergence dates. arXiv
- Morrison DA (2005) Bayesian posterior probabilities: revisited. arXiv
- Jenkins M, Morrison DA, Auld TD (2005) Estimating seed bank accumulation and patterns in three obligate-seeder Proteaceae species. arXiv
- Morrison DA (2009) How and where to look for tRNAs in Metazoan mitochondrial genomes, and what you might find when you get there. arXiv
- Kelk S, Linz S, Morrison DA (2013) Fighting network space: it is time for an SQL-type language to filter phylogenetic networks. arXiv
They have all been indexed by search engines such as Google, and they are thus available via Google Scholar (which also keeps track of citations of preprint papers), as well as via professional sites such as ResearchGate. In this sense, the data and ideas are just as "available" as they would be in any peer-reviewed publication, and potential "scholarly impact" is not compromised. Indeed, Twitter mentions of arXiv papers are recognized as being a powerful means of disseminating their content, irrespective of later publication (see How the scientific community reacts to newly submitted preprints: article downloads, twitter mentions, and citations). I even know of bioinformatics papers that were still being cited via the online pre-print (labeled as a "Technical Report") long after they finally made it into print.
So, preprint archives are a valuable tool for academics, especially when those pesky referees are not being co-operative.
PS. This is post number 200 for this blog.
Labels:
Archive
Wednesday, November 27, 2013
Within-species networks
In this blog we have consistently championed the idea that within-species relationships are better represented by a network than by a tree. We have done this for humans and their relatives:
Networks and human inter-population variationand for other species as well:
Human races, networks and fuzzy clusters
Why do we still use trees for the Neandertal genealogy?
Are phylogenetic trees useful for domesticated organisms?Genetically, a within-species network is a haplotype network. Also, when dealing with individuals in a sexually reproducing species it is a hybridization network, as I have noted:
Why do we still use trees for the dog genealogy?
Network of apple cultivars
Family trees, pedigrees and hybridization networksWe are not the only blog to emphasize intra-species networks, of course. As far as humans are concerned, one of the more vocal blogs has been Gene Expression, run by Razib Khan over at Discover magazine. For example, when discussing phylogenetic trees (Burning down the trees in historical population genetics), Khan notes:
Charles Darwin's family pedigree network
Toulouse-Lautrec: family trees and networks
These sorts of trees range from Ernst Haeckel's classical attempt, depicting relationships which biologists derived from intuition within the framework of a grand evolutionary scheme, all the way down to modern methods implemented in software packages such as Mr. Bayes, which many frankly utilize in a "turnkey" manner. These trees are abstractions, in that they reduce down a wide range of phenomena into schematic representations which impart aspects of particular interest in a stylized form. This is important, because the actual nature of the phenomena being represented may be more complex than is being represented.
Phylogenetic analysis involving distinct species has its own problems, but they are dwarfed by what must confront those who attempt to parse out relatedness of populations within species. Because of the ubiquity of gene flow across populations within species, attempts to generate a tree of relationships of populations is always bound to be a gross simplification. Instead of a sequence of bifurcations the true relationship of putative populations is more accurately represented by a networked graph.When discussing alternative evolutionary models (Unveiling the genealogical lattice), Khan notes:
It seems that the bifurcating model of the tree must now be strongly tinted by the shades of reticulation. In a stylized sense inter-specific phylogenies, which assume the approximate truth of the biological species concept (i.e., little gene flow across lineages), mislead us when we think of the phylogeny of species on the microevolutionary scale of population genetics. On an intra-specific scale gene flow is not just a nuisance parameter in the model, it is an essential phenomenon which must be accommodated into the framework.
And here the takeaway for me is that we may need to rethink our whole conception of pure ancestral populations, and imagine a human phylogenetic tree as a series of lattices in eternal flux, with admixed nodes periodically expanding so as to generate the artifice of a diversifying tree. The closer we look, the more likely it seems that most of the populations which have undergone demographic expansion in the past 10,000 years are also the products of admixture. Any story of the past 10,000 years, and likely the past 100,000 years, must give space at the center of the narrative arc to lateral gene flow across populations.Mind you, the network and lattice metaphors are not the only ones he has up his sleeve (When trees turn into brambles):
With the expansion of genomics from humans to a wide range of species I suspect that we’ll see a lot more blurring of distinctions between species on the margins. This will be particularly true of those lineages with wide and continuous distributions. It will also be most salient and surprising for mammalian populations, where our prejudices about the primacy of a biological species concept are most strongly developed. In a phylogenetic sense when you shift the grain of analysis to a finer scale the tree of life becomes much more of a bramble in many cases.Indeed.
Labels:
Haplotype network,
Hybridization network,
Phylogeny
Monday, November 25, 2013
Toulouse-Lautrec: family trees and networks
In a previous blog post (Charles Darwin's family pedigree network), I mentioned several well-known people who were involved in a consanguineous marriage, which is defined as the union of two people who are related as closer than second cousins. In that post I discussed in detail Charles Darwin (who married his first cousin); and in this post I discuss the artist Henri Toulouse-Lautrec, who was the offspring of a marriage between first cousins.
I thought that this would be a simple post, because there must be people who have studied the Toulouse-Lautrec-Montfa genealogy, given Henri's fame as a Post-Impressionist artist, along with the widespread knowledge that his phyiscal disabilities were genetic. But it turned out not to be so — there is no broad family tree that I could find, and no detailed discussion of inbreeding. The main information easily available is the direct lineage of inheritance of the various noble titles to which Henri would have been heir (had he survived his father, the Comte de Toulouse-Lautrec-Montfa), which can be traced back for more than 1000 years (see Vizegrafschaft Lautrec). However, the main interest for biology lies in his genetic relationship with his cousins, as we shall see below.
So, I sat down for a day to compile the family history for myself. The resulting genealogy is incomplete, but all of the relevant people are in it. I could not find all of the details about some of these people, either, which are apparently not available on the web; and some of the actual dates are inconsistent across different sources. In general, I have followed Dupic (2012).
When genealogical trees become networks
The point of this post is that marriages within a family turn the family tree into a network. So, a pedigree can be tree-like or not. In the latter case it is an example of a hybridization network.
This first genealogy shows a standard family tree for a single individual, looking backward in time from the bottom. So, this person is #1, the parents are #2 (father) and #3 (mother), and so on back through the generations, always with the male parent on the left (as is the convention). This example covers six generations, showing that without inbreeding everyone has 32 great-great-great grand-parents. These 32 people's genes are mixed more-or-less randomly (depending on recombination and assortment) to produce person #1. This is a good thing, evolutionarily, because there is then genetic diversity within #1.
However, with inbreeding some part of the ancestry disappears (when looking backward in time), because another part of the ancestry is duplicated in its place (this is called "pedigree collapse").
The second genealogy shows what happens when person #7 is the daughter of someone else in the same pedigree. If she is the daughter of #10 and #11, for example, then #5 and #7 would be sisters, and #2 and #3 would be first cousins. Now, person #1 has only 24 great-great-great grand-parents, and some of them are contributing to their descendants twice, rather than once (ie. #40–#47). This means that the genetic diversity in person #1 is less than it would be without the inbreeding. More to the point, any recessive alleles that exist in the ancestry have an increased probability of being homozygous in #1, and thus being expressed in the phenotype.
Toulouse-Lautrec's ancestry
This is, unfortunately, exactly what happened to Henri Toulouse-Lautrec, whose pedigree network is shown in the next figure. It is complete for six generations, plus an important part of the seventh. It is difficult to be complete beyond this generation, as the information becomes sparse, particularly about the female family members.
As shown, Henri's parents were first cousins, because their mothers were sisters. In addition, his maternal grandfather (#6) also had recent inbreeding in his history, because his mother (#13) was the daughter of a first-cousin marriage. This is not nearly as much inbreeding as has been implied by most commentators about Henri's life, but it is enough to potentially create genetic problems.
Note that it was Henri's mother's side of the family that was involved in the recent inbreeding, but the de Toulouse-Lautrec Montfa side was prone to the same thing, as are most titled families. As noted above, Henri died before inheriting his title. The title Comte de Toulouse-Lautrec-Monfa passed to Alphonse' next brother, Charles (1840-1917), who had no children, and thence to the next brother, Odon (1842-1937), and finally to Odon's son, Robert (1887-1972), who also had no children. The Internet seems to be silent about what happened to it after that.
Consequences of inbreeding
For Henri, life was tragic because he ended up with two copies of one particular recessive allele. The medical profession has been interested in this ever since his death, and much information is therefore now available about his condition (eg. Albury & Weisz 2013; Leigh 2013).
Albury & Weisz (2013) note:
The condition from which he probably suffered was first described in 1954 by the French physician Robert Weissman-Netter. It was named pycnodysostosis in 1962 by Marateaux and Lamy and was soon attributed to this artist as the "Toulouse-Lautrec Syndrome" ... Pycnodysostosis is a hereditary autosomal recessive dysplasia caused by an enzyme deficiency, namely of cathepsin K (cysteine protease deficiency in osteoclasts), reducing the normal bone resorption and leaving an incomplete matrix decomposition ... Toulouse Lautrec had a short stature with shortened legs, a large head due to a lack of closure of the fontanellae (which he usually covered with a hat), a shortened mandible with an obtuse angle (covered with a thick beard), dental deformities that required several surgical interventions, a large tongue, thick lips, profuse salivation, and a sinus obstruction with post-nasal drip. With fractures of the long bones during childhood, later on of the clavicle, with progressive hearing problems and cranio-facial deformities, Lautrec’s condition would complete the diagnosis of pycnodysostosis.It seems to be widely recognized that Henri threw himself into his art at least partly to compensate for the psychological damage produced by his physical condition (he also became an alcoholic). As Leigh (2013) notes, his mother's side of the family had money (his father's side had a title but little money), and so Henri was financially free to do what he liked. He worked at a prodigious rate, and produced a life-time's worth of art in just 15 years — perhaps most famously his flamboyant lithograph posters (still as popular today as they were in his own time), but also oil paintings, watercolours, sculptures, ceramics and stained glass. He died at his mother's Château Malromé at age 36, after a stroke, but ultimately probably from tuberculosis (Albury & Weisz 2013).
Further inbreeding in the family
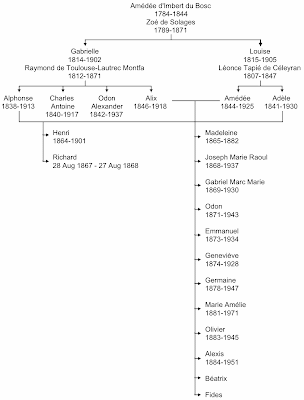
I noted in my previous post about Charles Darwin that, not only did he marry his cousin, his own sister married his wife's brother, thus literally keeping things in the family. In Henri Toulouse-Lautrec's case, the same thing happened: his paternal aunt married his maternal uncle, as shown in the next figure. This pedigree shows some more information about Henri's closest relatives, emphasizing the pair of consanguineous marriages.
There are 14 people shown in Henri's generation, all born to first-cousin marriages. (There may have been two more children in the Alix–Amédée marriage, but I have been unable to find any direct reference to them.) Of these people, six seem to have had disabilities similar to Henri's: Henri himself; his brother, who died the day before his first birthday; Madeleine, who died as a teenager; Geneviève; Béatrix; and Fides. The latter was so small that apparently she lived her entire life in a baby carriage (Rosenhek 2009). The photo below shows Henri with most of the Tapié de Céleyran family. It was taken in the summer of 1896 at Château du Bosc, where Henri had been born.
The two elderly women in the middle are Gabrielle (left) and Louise (right), the maternal and paternal grandmothers (they were sisters, remember). The father, Amédée, is at the rear centre (sticking his tongue out at the photographer), and the mother, Alix, is standing at the far right. Standing next to her is the oldest son, Raoul; and his wife, Elisabeth, is seated at the far left. The next two sons, Gabriel and Odon, are absent, along with their wives. The next son, Emmanuel, is standing at the back left; and his wife, Marie-Thérèse, is seated next to the pram (middle right). The youngest sons are sitting on the ground at the front centre, with Alexis on the left and Olivier on the right. The first-born daughter, Madeleine, was already dead when the photo was taken. The next three daughters are sitting at the middle left, with Germaine sitting on Elisabeth's lap, Geneviève in front of her, and then Marie seated on the ground. Béatrix is at the middle right, sitting next to Marie-Thérèse, and Fides is in her pram. Henri himself is seated on the ground at the far left. His brother, Richard, had also died before the photo was taken. The remaining four people (standing either side of Amédée) are other relatives.Nevertheless, this large family did manage to survive the effects of inbreeding, unlike Henri's own family. At least seven of the children survived to have children of their own (~19 grand-children):
| Person Raoul Gabriel Odon Emmanuel Germaine Marie Alexis |
Spouse Elisabeth DAUDÉ de LAVALETTE (1870-1956) Anne de TOULOUSE-LAUTREC (1873-1944) Marguerite TAILLEFER de LAPORTALIÈRE (1878-1958) Marie-Thérèse des CORDES Alexandre d'ANSELME (1876-1912) Adrien de RODAT d'OLEMPS (1806-1884) Anne Marie de MALVIN de MONTAZET (1885-1974) |
4 children 3 children 1 child 2 children 2 children 3 children 4 children |
Inbreeding increases the probability that recessive alleles will be expressed, but it does not make this inevitable. In Henri's case, two disabled children in succession seems to have dissuaded his parents, and they separated, whereas his aunt and uncle had a healthy child the second time, and so they continued producing a family. However, these days it is not recommended that you marry any of your first cousins.
Conclusion
Evolution is about biodiversity at all hierarchical levels, not just between or within species, but within individuals as well. Average intra-individual genetic diversity reaches a maximum when the ancestry is tree-like, and reduces with each instance of inbreeding, which turns the tree into a network of increasingly greater complexity.
I have discussed an even more extreme example of consanguinity in a previous post (Family trees, pedigrees and hybridization networks), in which the inbreeding became so severe that the royal family lineage actually came to an end.
References
Albury WR, Weisz GM (2013) Toulouse-Lautrec and medicine: a triumph over infirmity. Hektoen International 5: 3.
Dupic S. (2012) Toulouse-Lautrec - Généalogie 87 le site de référence de la généalogie de la haute-vienne.
Leigh FW (2013) Henri Marie Raymond de Toulouse-Lautrec-Montfa (1864-1901): artistic genius and medical curiosity. Journal of Medical Biography 21: 19-25.
Rosenhek J (2009) Picture imperfect: tiny Henri de Toulouse-Lautrec’s talent – and troubles – were larger than life. Doctor's Review Oct 2009.
Labels:
Gene flow,
Genealogy,
Hybridization network,
Pedigree
Wednesday, November 20, 2013
Bioinformaticians look at bioinformatics
Bioinformatics as a term dates back to the 1970s, usually credited to Paulien Hogeweg, of the Bioinformatics group at Utrecht University, in The Netherlands, although it apparently did not make it into print until 1988 (Paulien Hogeweg. 1988. MIRROR beyond MIRROR, puddles of Life. In: Artificial Life, C. Langton, ed. Addison Wesley, pp. 297-315.).
In the 1990s the field expanded rapidly and became recognized as a discipline of its own, as a subset of computational science. However, Christos A. Ouzounis (2012. Rise and demise of bioinformatics? Promise and progress. PLoS Computational Biology 8: e1002487) has noted a distinct decrease in the use of the term itself, as shown by this graph.
Ouzounis recognizes three (admittedly artificial) periods in the history: Infancy (1996-2001), Adolescence (2002-2006) and Adulthood (2007-2011). Along the way, the practice of bioinformatics has received a lot of criticism. I have noted some of this before, in previous blog posts:
Poor bioinformatics?
Archiving of bioinformatics software
What is perhaps most important is that much of this criticism comes from bioinformaticians themselves, rather than from biologists. Moreover, this criticism does not seem to have had much effect on how bioinformatics is practiced, given the length of time over which it has been made.
For example, Carole Goble (2007. The seven deadly sins of bioinformatics. Keynote talk at the Bioinformatics Open Source Conference Special Interest Group at the 15th Annual International Conference on Intelligent Systems for Molecular Biology (ISMB 2007) in Vienna, July 2007) produced this list of what she called "intractable problems in bioinformatics":
1. Parochialism and insularity.
2. Exceptionalism.
3. Autonomy or death!
4. Vanity: pride and narcissism.
5. Monolith megalomania.
6. Scientific method sloth.
7. Instant gratification.
More recently, Manuel Corpas, Segun Fatumo & Reinhard Schneider (2012. How not to be a bioinformatician. Source Code for Biology and Medicine 7: 3) pointed out what they call "a series of disastrous practices in the bioinformatics field", which look very similar:
1. Stay low level at every level.
2. Be open source without being open.
3. Make tools that make no sense to biologists.
4. Do not provide a graphical user interface: command line is always more effective.
5. Make sure the output of your application is unreadable, unparseable and does not comply to any known standards.
6. Be unreachable and isolated.
7. Never maintain your databases, web services or any information that you may provide at any time.
8. Blindly believe in the predictions given, P-values or statistics.
9. Do not ever share your results and do not reuse.
10. Make your algorithm or analysis method irreproducible.
Labels:
Bioinformatics,
computational biology,
software
Monday, November 18, 2013
Language history and language weirdness
Native speakers of any language will judge the "difficulty" of another language by how much it differs from their own. For example, the Foreign Service Institute (FSI) of the U.S. Department of State lists five categories of increasing time taken for native English speakers to acquire "General Professional Proficiency" in other languages. This refers to an average, of course, and anyone may personally find one language or another more easy or difficult than others.
FSI Category I (the least time needed) includes most of the Germanic and Romance languages, since English was originally a Germanic language that received a huge Romance input after the Normans turned up in Britain in 1066. The exception is German itself, which is alone in Category II (needing longer), because of its more complex grammar. Category V (the longest time needed for proficiency) consists of Arabic, Cantonese, Japanese, Korean and Mandarin, with Japanese being considered the most difficult.
Most languages are in Category IV, including the rest of the Indo-European languages. The recognizably tougher ones in that group are the Uralic languages (Estonian, Finnish and Hungarian), because of their countless noun cases. Interestingly, Category III (easier than IV) consists of Indonesian, Malaysian and Swahili, which have no known historical connection to English — they just happen to have fewer linguistic differences than do the other languages.
And that is the point of this post — linguistic similarities don't necessarily reflect the evolutionary history of the languages. There are trees allegedly showing the genealogy of languages, because there is vertical transfer of information in the history of languages (generation to generation), but horizontal transfer has also been a powerful evolutionary force, as cultures come in contact with each other. The history of English, as noted above, shows both vertical (Germanic) and horizontal (Romance) influences. Language history is a reticulating network, not an evolutionary tree.
Just as importantly, though, languages can have coincidental similarities. There are, after all, not that many different ways of constructing a language, and there are reported to be ~6,900 distinct languages on this planet. So, chance similarities must abound — what in biology we would call parallelisms and convergences. This makes constructing the evolutionary history of languages difficult.
The complexity created by coincidences has lead some people to wonder about how "unusual" any one language might be. This can be defined as how many of its characteristics occur commonly in other languages, and how many of them occur more rarely. The most unusual languages will be those that have lots of the rare features; and we might call them linguistic outliers. The Idibon blog has already had a look at this topic (The weirdest languages), and here I reconsider their data in the light of a phylogenetic network.
The data
The original data come from the World Atlas of Language Structures, which describes itself as "a large database of structural (phonological, grammatical, lexical) properties of languages gathered by a team of 55 authors". There are apparently 2,676 different languages in the database, coded for 192 linguistic features. Sadly, the database is very sparse, so that most languages have not yet been coded for most of the features (there are 5–1,519 languages coded for each feature).
So, the Idibon people selected a subset of the data: 1,693 languages and 21 features. These features were chosen to be an uncorrelated subset of those 165 features that have at least 100 languages coded; and the selected languages each have at least 10 features coded.
The features are certainly an eclectic collection, which you can read about on the WALS site:
| 83A: 87A: 143A: 143G: 69A: 116A: 57A: 101A: 6A: 71A: 129A: 130A: 44A: 14A: 9A: 72A: 111A: 64A: 124A: 117A: 19A: |
Order of Object and Verb Order of Adjective and Noun Order of Negative Morpheme and Verb Minor Morphological Means of Signaling Negation Position of Tense-Aspect Affixes Polar Questions Position of Pronominal Possessive Affixes Expression of Pronominal Subjects Uvular Consonants The Prohibitive Hand and Arm Finger and Hand Gender Distinctions in Independent Personal Pronouns Fixed Stress Locations The Velar Nasal Imperative-Hortative Systems Nonperiphrastic Causative Constructions Nominal and Verbal Conjunction 'Want' Complement Subjects Predicative Possession Presence of Uncommon Consonants |
I then tried to fill in some of the missing data, to get as many languages as easily possible up to having 14 features coded (ie. two-thirds of the features). For the phonology features (6A, 9A, 19A), the relevant information can be looked up on the web, particularly in Wikipedia and the Native American Language Net. For the word features (129A, 130A), I used the LEXILOGOS Online Translation.
In the process, I found that Idibon has at least one feature mis-coded compared to the WALS web site: for feature 14A, some of the languages that should be coded "Second " have been coded as "Antepenultimate", and all of the others that should be coded "Second" have missing data.
I also found a few contradictions between the WALS coding and the information elsewhere on the web. In some of these cases I re-coded the WALS data.
My final spreadsheet is available online. There are 280 languages coded for at least 14 of the 21 features, compared to 239 such languages in the Idibon analysis. There are 19% of the data still missing, varying from 0–53% across the 21 features.
The network
My network is intended as an exploratory data analysis, rather than some attempt at an evolutionary diagram. Thus, the network simply displays the apparent similarity among the languages. That is, languages that are closely connected in the network are similar to each other based on their linguistic features, and those that are further apart are progressively more different from each other.
First, I recoded the multivariate linguistic data as 59 binary characters. Then the similarity among the 280 languages was calculated for each pair of languages using the Gower similarity index, which can accommodate missing data (by ignoring features that are missing for each pairwise comparison). A Neighbor-net analysis was then used to display the between-language similarities as a phylogenetic network.
The network is not very tree-like, is it? A few tentative groups can be recognized, as indicated by my colouring, but that is all. These groups do not correspond to any known language groups, meaning that the language features chosen do not reveal a traditional tree-like genealogy. Whether this reflects horizontal transfer of linguistic features, coincidence, or simply inadequate data, is not necessarily clear.
However, it seems most likely that much of the complexity represents coincidence. In the study of language evolution, parallelism and convergence are not nuisances, which is the way they are treated when constructing phylogenies of organisms. Coincidental similarities are a fundamental part of language history, but they are not necessarily the product of processes like natural selection, as they often are in biology.
If we look at some of the details, the nature of the complexity becomes clearer, as shown in the next figure. Here, I have colour-coded the Indo-European family of languages by their so-called "genus", plus the other languages that occur in Europe (the Uralic group, and Basque):
| Albanian - pale brown Armenian - dark brown Baltic - orange |
Celtic - pale blue Germanic - black Greek - pale green |
Indic - pink Iranian - blue Romance - purple |
Slavic - green Uralic - red Basque - grey |
Note that the seven Germanic languages are clustered in a single location, as are the two Baltic languages. The others appear in either two (Celtic, Romance, Iranian) or four (Indic, Slavic, Uralic) locations. This implies considerable linguistic variation within most of what are considered to be closely related languages (that is why they are called language genera). A larger collection of features might change the pattern, of course, but I still reckon that there is a large component of non-vertical transmission here. This is either coincidence or horizontal transmission. For the Indo-European languages, the latter is perhaps quite likely; but it is equally likely that it is simply coincidence, even at this relatively fine scale.
The weirdest languages
The Idibon blog tried to reduce the multivariate data down to a single number for each language (scaled 0–1), representing its "weirdness" in terms of how many uncommon features it has. So, I have performed the same calculation for my expanded dataset.
The complete list is in the spreadsheet, but here are the top and bottom most-unusual languages:
| Top 20 Mixtec (Chalcatongo) Seri Nenets Diegueño (Mesa Grande) Oromo (Harar) Choctaw Kutenai Iraqw Danish Kongo Norwegian Dutch Swedish German Armenian (Eastern) Abkhaz Mumuye Ju|'hoan Khoekhoe Ladakhi |
0.9725 0.9354 0.9346 0.9196 0.9187 0.9138 0.9079 0.9005 0.8843 0.8830 0.8751 0.8705 0.8585 0.8581 0.8473 0.8445 0.8410 0.8346 0.8300 0.8247 |
Bottom 20 Kanuri Kunama Kiowa Marathi Khanty Turkish Bulgarian Wichita Manam Kewa Sentani Bororo Usan Cantonese Hungarian Chamorro Ainu Cherokee Purépecha Hindi |
0.2410 0.2401 0.2361 0.2752 0.2149 0.2145 0.2112 0.2054 0.2085 0.1984 0.1952 0.1534 0.1508 0.1435 0.1316 0.1285 0.1277 0.1232 0.0997 0.0872 |
Nevertheless, it is worth noting that five of the seven Germanic languages are in the top 15 (plus English is at 40 and Icelandic 47). Unusually, most of the Germanic languages still use cases (modifications to words that show how they relate to other words in a sentence). This means that you have to memorize a lot of different versions of each noun, just as you do in Latin. Moreover, these languages change the word order when asking a question as opposed to making a statement, whereas most languages add a participle instead. (In the most unusual language, Mixtec, a native language from Mexico, there is apparently no difference between a question and statement!)
English has a lower score than other Germanic languages presumably because of the French influence mentioned above (French is ranked 42). For example, in English there are now very few cases (only for some pronouns), as in the other Germanic languages, but instead it uses a fairly strict word order to express grammatical relationships. (You will note that two of the English-speaking authors of this blog now live in countries with other Germanic languages, and so we know just how big a pain it is to learn illogical case endings.)
English does have one really odd feature, though, which is the use of the sound "th" (which is part of feature 19A). There are two forms of this sound, voiced (as in "the") and unvoiced (as in "thing"). These sounds do not exist in most languages, and they are rare even among the other Indo-European languages. That is why you often hear non-native speakers say "dis" and "zis" instead of "this" — "th" is a sound that they have no experience making.
Actually, the Indo-European languages are very diverse in their weirdness. Many of them are at the top of the list, but there are also some at the bottom, including Hindi which is dead last. Notably, three of the Romance languages are at the top (Spanish, Portuguese, French) and two are at the bottom (Romanian, Italian). This seems unlikely, given the overall similarity of Spanish and Italian, for example; and so it probably reflects the specific choice of linguistic features.
The data are also potentially sensitive to some of the feature coding. One notable example is for feature 19A in Arabic. WALS codes Arabic as having pharyngeals but not "th", while Wikipedia says that the pharyngeals are doubtful, but that Arabic has "th". So, the possble codings of Arabic, and their resulting weirdness, are:
| Feature "Th" sounds only Pharyngeals only Pharyngeals and "th" |
Score 0.0893 0.0469 0.0045 |
Weirdness 0.6788 0.7416 0.9245 |
Conclusion
Languages do not have a tree-like evolutionary history. Even the relatively small dataset presented here seems to show the influence of horizontal evolution. But, more importantly, we should not underestimate the coincidental occurrence of language features (parallelism and convergence). These have usually been treated as a nuisance in phylogenetic studies of organisms, but they are likely to be important for the study of languages. I have discussed this further in a previous post (False analogies between anthropology and biology).
Labels:
EDA,
Linguistics
Subscribe to:
Posts (Atom)