Wednesday, April 30, 2014
Reconstructing ancestors in a splits network?
A splits graph is an unrooted phylogenetic network (see How to interpret splits graphs). However, sometimes they are treated as being rooted networks, and under these circumstances it is assumed that they therefore represent a phylogeny. Nevetheless, it is important to recognize that a rooted splits graph does not explicitly represent a phylogeny, because reticulations in the graph represent uncertainty not genealogy (see How do we interpret a rooted haplotype network?).
A corollary to this is that reconstructing "ancestors" in a splits graph is problematic. The nodes do not necessarily represent inferred ancestors, because their actual role is to support the corners of the parallelograms formed by intersecting sets of parallel edges in the graph. Some of the nodes may, indeed, represent ancestors but there is no way to determine this from the network itself.
An example
Let's look at a specific example, taken from the paper by J. Miguel Díaz-Báñez, Giovanna Farigu, Francisco Gómez, David Rappaport & Godfried T. Toussaint (2004) El Compás flamenco: a phylogenetic analysis. Proceedings of BRIDGES Conference: Mathematical Connections in Art, Music and Science, pp. 61-70.
The authors provide an analysis of the hand-clapping patterns of the flamenco music of Andalucia, in southern Spain. There are four recognized patterns, plus the fandango pattern, and the authors use two different distance measures to assess their rhythmic similarities. They produce unrooted phylogenetic networks based on each of these distances, which turn out (on reanalysis of their data) to be NeighborNets (the authors refer to them as "SplitsTrees").
The authors ignore the fact that "it is well established that the fountain of flamenco music is the fandango", which would make the fandango the outgroup for rooting if we did wish to treat the networks as rooted. Instead, they try to "reconstruct the 'ancestral' rhythms corresponding to the nodes" by using mid-point rooting. This procedure can easily be applied to unrooted phylogenetic trees, but its application to networks is problematic because there are multiple paths through the graph, and there may thus be several points that qualify as the mid-point.
For one of their networks, shown in the first graph, the authors identify the single mid-point, and then try to reconstruct "the ancestral rhythm closest to the 'center'", based on the node closest to the mid-point. They do this by "trial and error", based on the distances from the identified "ancestral" node to all of the leaves. That is, they find the hand-clap pattern that has the required distance to all of the leaves.
The authors do not tackle this procedure for their other network. In this case, as shown in the next graph, there are two mid-point locations. While there is a node that is equally close to these two locations, which might therefore qualify as "the ancestral rhythm closest to the center", it is difficult to reconstruct its actual rhythm.
Finally, if we try to identify the "ancestral rhythm" using the node identified by the fandango outgroup, then the result is dramatically different to that produced by the mid-point method, for both networks.
Labels:
Rooting,
Splits graph
Sunday, April 27, 2014
The first HGT network
I have published a number of blog posts about early phylogenetics involving horizontal gene transfer (HGT). The historical issue is that all of the early publications about HGT of individual genes were about mechanisms and evidence, rather than about the phylogeny, and so explicit network illustrations were rare. It is therefore difficult to pinpoint the first illustrated network.
For example, if we consider HGT to be a subset of genome transfer (or genome fusion) then the first explicit phylogenetic network illustrating this was by Constantin Mereschkowsky (1910) Theorie der zwei Plasmaarten als Grundlage der Symbiogenese, einer neuen Lehre von der Entstehung der Organismen. Biologisches Centralblatt 30: 278–303, 321–347, 353–367 (see The first gene transfer network). However, HGT is conventionally treated as involving a small collection of genes, not whole genomes.
Alternatively, if we consider unrooted phenograms to represent HGT networks, then the first explicit illustration of relationships based on individual genes was by Dorothy Jones & Peter H. Sneath (1970) Genetic transfer and bacterial taxonomy. Bacteriology Reviews 34: 40-81 (HGT networks). However, phenetics is not really phylogenetics.
It seems that if we insist upon an illustration showing a rooted phylogenetic network, then we must turn to the paper by Raoul E. Benveniste & George J. Todaro (1974) Evolution of C-type viral genes: inheritance of exogenously acquired viral genes. Nature 252: 456-459. The summary of this paper is:
Genes related to the nucleic acid of an endogenous domestic cat C-type virus (RD114) are found in the cellular DNA of anthropoid primates while many members of the cat family Felidae lack these sequences. Endogenous viruses from primates are thus concluded to have infected and become part of the germ line of an evolutionarily distance group, the ancestors of the domestic cat.The authors discuss HGT explicitly in the context of a phylogeny:
When the virogenes of two species are more closely related to each other than are the cellular genes, one must suspect horizontal transmission and subsequent perpetuation of the viral genes through the germ line. Figure 3 shows models which could account for the data.
There are three distinct phylogenetic models in this figure, and the third one has three alternative possibilities. The authors conclude that "model cII is most likely." This then appears to be the first HGT network that fits the conventional specifications.
Labels:
HGT network,
History
Tuesday, April 22, 2014
Do phylogenetic networks support Intelligent Design?
It is always interesting to see what the media make of scientific publications. Some time ago, several of us were involved in a paper in Trends in Genetics advocating the more widespread use of phylogenetic networks (Networks: expanding evolutionary thinking), which seemed mild enough. For example, the Idaho State University press release about the paper made it onto the Phys.Org news site reasonably accurately (Amending the Tree of Life).
However, the Intelligent Design site Evolution News and Views had a different take on things (Demolishing Darwin's Tree), reaching a series of conclusions that might
One can only welcome this paper's bold proposal to overturn entrenched dogma ... the "network" diagram seems conducive to ID research inasmuch as it calls into question universal common ancestry via natural selection (i.e., neo-Darwinism), and seeks to portray the evidence honestly ... It's too soon to tell if Darwin security forces will let this band of independent thinkers gather a following. If nothing else, it shows (notwithstanding the insistences of the National Center for Science Education) that insiders know about the fundamental controversies in evolutionary theory, and are calling for some of the same reforms that advocates of intelligent design do.I am not sure that all of these conclusions are logically consistent with the words of the original paper.
Wednesday, April 16, 2014
Some things you probably don't know about the bootstrap
The following text was written a few years ago, but much of it never got published. So, I thought that this might be a good opportunity to make it available, since what it says is still true today.
Since a phylogenetic tree is interpreted in terms of the monophyletic groups that it hypothesizes, it is important to quantitatively assess the robustness of all of these groups (i.e. the degree of support for each branch in the tree) — is the support for a particular group any better than would be expected from a random data set? This issue of clade robustness is the same as assessing branch support on the tree, since each branch represents a clade. Many different techniques have been developed, including:
- analytical procedures, such as interior-branch tests (Nei et al. 1985; Sneath 1986), likelihood-ratio tests (Felsenstein 1988; Huelsenbeck et al. 1996b), and clade significance (Lee 2000);
- resampling procedures, such as the bootstrap (Felsenstein 1985), the jackknife (Lanyon 1985), topology-dependent permutation (Faith 1991), and clade credibility or posterior probability (Larget and Simon 1999); and
- non-statistical procedures, such as the decay index (Bremer 1988), clade stability (Davis 1993), and spectral signals (Hendy and Penny 1993).
The bootstrap
This method was first introduced by Efron (1979) as an alternative method to jackknifing for producing standard errors on estimates of central location other than the mean (e.g. the median), but it has since been expanded to cover probabilistic confidence intervals as well (Efron and Tibshirani 1993; Davison and Hinkley 1997). It was introduced into phylogenetic studies by Penny et al. (1982) and then formalized by Felsenstein (1985), who suggested that it could be implemented by holding the taxa constant and resampling the characters randomly with replacement, the tree-building analysis then being applied to each of the bootstrap resamples.
Bootstrapping is a monte carlo procedure that generates "pseudo" data sets from the original data, and then uses these new data sets for its inferences. That is, it tries to derive the population inferences (i.e the "true" answer) from repeated generation of new samples, each sample being constrained by the characteristics of the original data sample. It thus relies on an explicit analogy between the sample and the appropriate population: that sampling from the sample is the same as sampling from the population. Clearly, the strongest requirement for bootstrapping to work is that the sample be a reasonable representation of the population.
Bootstrap confidence intervals are only ever approximate, especially for complex data structures, as they are a fundamentally more ambitious measure of accuracy than is a simple standard error (SE). For example, the usual formula for calculating a confidence interval (CI) when the population frequency distribution is assumed to be normal is: CI = t * SE, where t is the Student t-value associated with the particular sample size and confidence percentage required. However, the main use of bootstrapping is in situations where the population frequency distribution is either indeterminate or is difficult to obtain empirically, and so this simple formula cannot be applied. Getting from the standard error to a confidence interval is then not straightforward. As a result, there are actually several quite distinct procedures for performing bootstrapping (Carpenter and Bithell 2000), with varying degrees of expected success.
Types of bootstrap
The original technique is called the percentile bootstrap. It is based on the principle of using the minimum number of ad hoc assumptions, and so it merely counts the percentage of bootstrap resamples that meet the specified criteria. F§or example, to estimate the standard error of a median, the median can be calculated for each bootstrap resample and then the standard deviation of the resulting frequency distribution will be the estimated standard error of the original median. The method is thus rather simplistic, and is often referred to as the naïve bootstrap, because it assumes no knowledge of how to calculate population estimates. It is a widespread method, as it can be applied even when the other methods cannot. However, it is known to have certain problems associated with the estimates produced, particularly for confidence intervals, such as bias and skewness (especially when the parent frequency distribution is not symmetrical). These were pointed out right from the start (Efron 1979), and efforts have subsequently been made to deal with them. Nevertheless, this is the form of bootstrap introduced by Felsenstein (1985), and it is the one used by most phylogeny computer programs. It is therefore the one that will be discussed in more detail below.
These known problems with the naïve bootstrap can be overcome by using bias-corrected (BC) bootstrap estimates — that is, the bias is estimated and removed from the calculation of the confidence interval. Possible dependence of the standard error on the parameter being estimated, which creates skewness, can be dealt with by using bias-corrected and accelerated (BCa) bootstrap estimates, so that the bias and skewness are both estimated and removed from the calculation of the confidence interval. The BCa method is the one usually recommended for use (Carpenter and Bithell 2000), because it corrects for both bias and skewness. This method is much slower to calculate than the simple percentile bootstrap, because it requires an extra parameter to be estimated for each of the bias and skewness corrections, and the latter correction is actually estimated by performing a separate jackknife analysis on each bootstrap resample (which means that the analysis can take 100 times as long as a naïve analysis). There have been several attempts to apply this form of correction methodology to bootstrapping in a phylogenetic context (Rodrigo 1993; Zharkikh and Li 1995; Efron et al. 1996; Shimodaira 2002), but while these can be successful at correcting bias and skewness (Sanderson and Wojciechowski 2000) these have not caught on, possibly because of the time factor involved.
Alternatively, we can decide not to be naïve when calculating confidence intervals, and to therefore calculate them in the traditional manner, using the standard error and the t-distribution. However, we then need to overcome any non-normal distribution problems of these two estimates by estimating both of them using bootstrapping. That is, bootstrapped-t confidence intervals are derived by calculating both the standard error and the t-value using bootstrapping, and then calculating the confidence interval as ±t * SE. To many people, this is the most natural way to calculate confidence intervals, since it matches the usual parametric procedure, and thus it is frequently recommended (Carpenter and Bithell 2000). Once again, this method is much slower to calculate than the percentile bootstrap, because the t-value is actually estimated by performing a separate bootstrap analysis on each bootstrap resample (which means that the analysis can take 100 times as long as a naïve analysis). This methodology seems not to have yet been suggested in a phylogenetic context, and in any case the time factor may be restrictive.
It is also possible to calculate test-inversion confidence intervals. This idea is based on the reciprocal relationship of statistical tests and confidence intervals, where (for example) non-overlapping 95% confidence intervals indicate statistically significant patterns at p<0.05 and vice versa. Thus, if we work out the situation where the pattern has a probability of p=0.05 of occurring by chance, then this defines the 95% confidence limit of the pattern. Clearly, this can be a complex process, especially for two-sided tests (which double the required number of calculations), as it can only be done by iteratively modifying the pattern and re-calculating the probability until the solution is reached. Once again, no-one yet seems to have suggested this methodology in a phylogenetic context, which is not unexpected given the general problems in deciding how to test branches statistically.
The above methods all count as non-parametric bootstrap methods. More recently, parametric bootstrapping methods have also been developed, which make the more restrictive assumption that a parametric model can be applied to the data (e.g. that the standard deviation of the parameter can be reliably estimated). In parametric bootstrapping we generate simulated datasets based on the assumed frequency distribution of the data, rather than by resampling from the data set itself. That is, instead of sampling from the sample, we sample from the assumed theoretical distribution to generate the set of bootstrap samples. We can then apply the percentile, BCa or bootstrap-t methods, described above, in the usual way. Clearly this method assumes that we know the appropriate frequency distribution; and the method will only be appropriate if this assumption is true, but not otherwise. However, if the assumption is correct, then this can be the most powerful method (Huelsenbeck et al. 1996a; Newton 1996) because it is not dependent on the representativeness of the data sample. The method has been introduced into phylogenetics in several contexts (Goldman 1993; Adell and Dopazo 1994; Huelsenbeck et al. 1996a), but the appropriate frequency distribution for branch support is not obvious (i.e. a phylogeny is a complex structure and cannot be represented by a single number but rather requires a model of sequence evolution and a model tree) and so it is not used for this purpose.
Issues with the bootstrap
Thus, for several reasons, all of the best bootstrapping methods are not likely to be available when assessing the robustness of a phylogenetic tree, and we are left with the naïve percentile bootstrap, which can be expected a priori to provide biased and skewed estimates of confidence intervals (because the frequency distribution associated with tree branches will not be symmetrical). Sadly, these problems have been repeatedly confirmed for the assessment of branch support in phylogenetic tree-building, both theoretically (Zharkikh and Li 1992a, 1992b; Felsenstein and Kishino 1993; Li and Zharkikh 1994; Sitnikova et al. 1995; Berry and Gascuel 1996; Efron et al. 1996; Huelsenbeck et al. 1996a; Newton 1996; Sanderson and Wojciechowski 2000; Suzuki et al. 2002; Alfaro et al. 2003; Erixon et al. 2003; Galtier 2004; Huelsenbeck and Rannala 2004) and empirically (Sanderson 1989; Hillis and Bull 1993; Buckley et al. 2001; Buckley and Cunningham 2002; Wilcox et al. 2002; Taylor and Piel 2004).
These studies have demonstrated that the probability of bootstrap resampling supporting the true tree may be either under- or overestimated, depending on the particular situation. For example, bootstrap values >75% tend to be underestimates of the amount of support, while they may be overestimates below this level, as shown in the first graph (above). That is, when the branch support is strong (i.e. the clade is part of the true tree) there will be an underestimation and when the support is weak (i.e. the clade is not part of the true tree) there will be an overestimation. This situation has been reported time and time again, with various theoretical explanations (e.g. Felsenstein and Kishino 1993; Efron et al. 1996; Newton 1996), although there are dissenting voices (e.g. Taylor and Piel 2004) as would be expected for a complex situation. Unfortunately, practitioners seem to ignore this fact, and to assume incorrectly that bootstrap values are always underestimates.
Just as importantly, the theoretical studies show that the pattern of over- and underestimation depends on (i) the shape of the tree and the branch lengths, (ii) the number of taxa, (iii) the number of characters, (iv) the evolutionary model used, and (v) the number of bootstrap resamples. This was first reported by Zharkikh and Li (1992a), and has been reconfirmed since then. For example, with few characters the bootstrap index tends to overestimate the support for a clade and to underestimate it for more characters. This is particularly true if the number of phylogenetically informative characters is increased or the number of non-independent characters is increased; and the index becomes progressively more conservative (i.e. lower values) as the number of taxa is increased.
Moreover, these patterns of under- and overestimation are increased with an increasing number of bootstrap replications, as shown in the next graph — this called "being wrong, with confidence".
The following graph pair of graphs show the effect of varying the evolutionary model used to generate the data, where under-specification of the analysis model leads to a general over-estimate of the true probability (cross-over at p=0.8, as shown in the first graph of the pair), while matching the generating and analysis models leads to a general under-estimation (cross-over at p=0.3, as shown in the second graph of the pair).
These are serious issues, which seem to be often ignored by practitioners. We can't just assume that the "true" support value is larger than our observed bootstrap value. In particular, this means that bootstrap values are not directly comparable between trees, even for the same taxa, and thus there can be no "agreed" level of bootstrap support that can be considered to be "statistically significant". A bootstrap value of 90% on a branch on one tree may actually represent less support than a bootstrap value of 85% on another tree, depending on the characteristics of the dataset concerned and the bootstrapping procedure used (although within a single tree the values should be comparable).
This complex situation means that we have to consider carefully how best to interpret bootstrap values in a phylogenetic context (Sanderson 1995). The bootstrap proportion (i.e. the proportion of resampled trees containing the branch/clade of interest) has variously been interpreted as (Berry and Gascuel 1996):
- a measure of reliability, telling us what would be expected to happen if we repeated our experiment;
- a measure of accuracy, telling us about the probability of our experimental result being true; and
- a measure of confidence, interpreted as a conditional probability similar to those in standard statistical hypothesis tests (i.e. measuring Type I errors or false positives).
The issue of support values depending on the number of bootstrap replicates is also of interest. It is usually recommended that at least 1,000–2,000 bootstrap resamples are taken for estimating confidence intervals, and this generality has been applied to phylogenetic trees (Hedges 1992). However, it is important to recognize that these suggestions relate to the precision of the confidence estimates not to their accuracy. Accuracy refers to how close the estimates are to the true value (i.e. correctness) while precision refers to how variable are the estimates (i.e. repeatability). Accuracy depends on a complex set of characteristics many of which have nothing to do with bootstrap replication. Precision, on the other hand, is entirely to do with the number of bootstrap replicates and the expected accuracy of the estimates. As shown in the next graph, 100 replicates at a conventional level of accuracy produces estimates that are expected to be within ±4% of the "true" values while 2,000 replicates produces estimates ±1%. This needs to be borne in mind when deciding whether to call a particular value "significant support" or not.
There have also been attempts to overcome some of the practical limitations of bootstrapping for large data sets by adopting heuristic procedures, including resampling estimated likelihoods for maximum-likelihood analyses (Waddell et al. 2002) and reduced tree-search effort for the bootstrap replicates. However, approaches using reduced tree-search effort produce even more conservative estimates of branch support, and the magnitude of the effect increases with decreasing bootstrap values (DeBry and Olmstead 2000; Mort et al. 2000; Sanderson and Wojciechowski 2000).
References
Adell J.C., Dopazo J. 1994. Monte Carlo simulation in phylogenies: an application to test the constancy of evolutionary rates. J. Mol. Evol. 38, 305-309.
Alfaro M.E., Zoller S., Lutzoni F. 2003. Bayes or bootstrap? A simulation study comparing the performance of bayesian markov chain monte carlo sampling and bootstrapping in assessing phylogenetic confidence. Mol. Biol. Evol. 20, 255-266.
Berry V., Gascuel O. 1996. On the interpretation of bootstrap trees: appropriate threshold of clade selection and induced gain. Mol. Biol. Evol. 13, 999-1011.
Bremer K. 1988. The limits of amino acid sequence data in angiosperm phylogenetic reconstruction. Evolution 42, 795-803.
Buckley T.R., Cunningham C.W. 2002. The effects of nucleotide substitution model assumptions on estimates of nonparametric bootstrap support. Mol. Biol. Evol. 19, 394-405.
Buckley T.R., Simon C., Chambers G.K. 2001. Exploring among-site rate variation models in a maximum likelihood framework using empirical data: effects of model assumptions on estimates of topology, branch lengths and bootstrap support. Syst. Biol. 50, 67-86.
Carpenter J., Bithell J. 2000. Bootstrap confidence intervals: when, which, what? A practical guide for medical statisticians. Stat. Med. 19, 1141-1164.
Davis J.I. 1993. Character removal as a means for assessing the stability of clades. Cladistics 9, 201-210.
Davison A.C., Hinkley D.V. 1997. Bootstrap Methods and Their Applications. Cambridge Uni. Press, Cambridge.
DeBry R.W., Olmstead R.G. 2000. A simulation study of reduced tree-search effort in bootstrap resampling analysis. Syst. Biol. 49, 171-179.
Efron B. 1979. Bootstrapping methods: another look at the jackknife. Ann. Stat. 7, 1-26.
Efron B., Halloran E., Holmes S. 1996. Bootstrap confidence levels for phylogenetic trees. Proc. Nat. Acad. Sci. U.S.A. 93, 7085-7090.
Efron B., Tibshirani R.J. 1993. An Introduction to the Bootstrap. Chapman & Hall, London.
Erixon P., Svennblad B., Britton T., Oxelman B. 2003. Reliability of bayesian probabilities and bootstrap frequencies in phylogenetics. Syst. Biol. 52, 665-673.
Faith D.P. 1991. Cladistic permutation tests for monophyly and nonmonophyly. Syst. Zool. 40, 366-375.
Felsenstein J. 1985. Confidence limits on phylogenies: an approach using the bootstrap. Evolution 39, 783-791.
Felsenstein J. 1988. Phylogenies from molecular sequences: inference and reliability. Annu. Rev. Genet. 22, 521-565.
Felsenstein J., Kishino H. 1993. Is there something wrong with the bootstrap on phylogenies? A reply to Hillis and Bull. Syst. Biol. 42, 193-200.
Galtier N. 2004. Sampling properties of the bootstrap support in molecular phylogeny: influence of nonindependence among sites. Syst. Biol. 53, 38-46.
Goldman N. 1993. Statistical tests of models of DNA substitution. J. Mol. Evol. 36, 182-198.
Goloboff P.A., Farris J.S., Källersjö M., Oxelman B., Ramırez M.J., Szumik C.A. 2003. Improvements to resampling measures of group support. Cladistics 19, 324-332.
Hedges S.B. 1992. The number of replications needed for accurate estimation of the bootstrap P value in phylogenetic studies. Mol. Biol. Evol. 9, 366-369.
Hendy M.D., Penny D. 1993. Spectral analysis of phylogenetic data. J. Classific. 10, 5-24.
Hillis D.M., Bull J.J. 1993. An empirical test of bootstrapping as a method for assessing confidence in phylogenetic analysis. Syst. Biol. 42, 182-192.
Holmes S. 2003. Bootstrapping phylogenetic trees: theory and methods. Statist. Sci. 18, 241-255.
Huelsenbeck J.P., Hillis D.M., Jones R. 1996a. Parametric bootstrapping in molecular phylogenetics: applications and performance. In: Ferraris, J.D., Palumbi, S.R. (Eds), Molecular
Huelsenbeck J.P., Hillis D.M., Nielsen R. 1996b. A likelihood ratio test of monophyly. Syst. Biol. 45, 546-558.
Huelsenbeck J.P., Rannala B. 2004. Frequentist properties of bayesian posterior probabilities of phylogenetic trees under simple and complex substitution models. Syst. Biol. 53, 904-913.
Lanyon S.M. 1985. Detecting internal inconsistencies in distance data. Syst. Zool. 34, 397-403.
Larget B., Simon D.L. 1999. Markov chain monte carlo algorithms for the bayesian analysis of phylogenetic trees. Mol. Biol. Evol. 16, 750-759.
Lee M.S.Y. 2000. Tree robustness and clade significance. Syst. Biol. 49, 829-836.
Li W.-H., Zharkikh A. 1994. What is the bootstrap technique? Syst. Biol. 43, 424-430.
Mort M.E., Soltis P.S., Soltis D.E., Mabry M.L. 2000. Comparison of three methods for estimating internal support on phylogenetic trees. Syst. Biol. 49, 160-171.
Nei M., Stevens J.C., Saitou M. 1985. Methods for computing the standard errors of branching points in an evolutionary tree and their application to molecular data from humans and apes. Mol. Biol. Evol. 2, 66-85.
Newton M.A. 1996. Bootstrapping phylogenies: large deviations and dispersion effects. Biometrika 83, 315-328.
Penny D., Foulds L.R., Hendy M.D. 1982. Testing the theory of evolution by comparing phylogenetic trees constructed from five different protein sequences. Nature 297, 197-200.
Rodrigo A.G. 1993. Calibrating the bootstrap test of monophyly. Int. J. Parasitol. 23, 507-514.
Sanderson M.J. 1989. Confidence limits on phylogenies: the bootstrap revisited. Cladistics 5, 113-129.
Sanderson M.J. 1995. Objections to bootstrapping phylogenies: a critique. Syst. Biol. 44, 299-320.
Sanderson M.J., Wojciechowski M.F. 2000. Improved bootstrap confidence limits in large-scale phylogenies, with an example from Neo-Astragalus (Leguminosae). Syst. Biol. 49, 671-685.
Shimodaira H. 2002. An approximately unbiased test of phylogenetic tree selection. Syst. Biol. 51, 492-508.
Sitnikova T., Rzhetsky A., Nei M. 1995. Interior-branch and bootstrap tests of phylogenetic trees. Mol. Biol. Evol. 12, 319-333.
Sneath P.H.A. 1986. Estimating uncertainty in evolutionary trees from Manhattan-distance triads. Syst. Zool. 35, 470–488.
Soltis P.S., Soltis D.E. 2003. Applying the bootstrap in phylogeny reconstruction. Statist. Sci. 18, 256-267.
Suzuki Y., Glazko G.V., Nei M. 2002. Overcredibility of molecular phylogenies obtained by bayesian phylogenetics. Proc. Nat. Acad. Sci. U.S.A. 99, 16138-16143.
Taylor D.J., Piel W.H. 2004. An assessment of accuracy, error, and conflict with support values from genome-scale phylogenetic data. Mol. Biol. Evol. 21, 1534-1537.
Waddell P.J., Kishino H. and Ota, R. 2002). Very fast algorithms for evaluating the stability of ML and Bayesian phylogenetic trees from se- quence data. Genome Informatics 13, 82-92.
Wilcox T.P., Zwickl D., Heath T.A., Hillis D.M. 2002. Phylogenetic relationships of the dwarf boas and a comparison of bayesian and bootstrap measures of phylogenetic support. Mol. Phylogenet. Evol. 25, 361-371.
Zharkikh A., Li W.-H. 1992a. Statistical properties of bootstrap estimation of phylogenetic variability from nucleotide sequences. I. Four taxa with a molecular clock. Mol. Biol. Evol. 9, 1119-1147.
Zharkikh A., Li W.-H. 1992b. Statistical properties of bootstrap estimation of phylogenetic variability from nucleotide sequences. II. Four taxa without a molecular clock. J. Mol. Evol. 35, 356-366.
Zharkikh A., Li W.-H. 1995. Estimation of confidence in phylogeny: the complete-and-partial bootstrap technique. Mol. Phylogenet. Evol. 4, 44-63.
Labels:
Bootstrap
Monday, April 14, 2014
The rise and fall of "David"
In Australia at the time I was born, the most popular first name for boys was "David" and the second most popular was "Andrew". Not unexpectedly, the most popular middle name was "Andrew" and number two was "David". It then comes as no surprise to you that I ended up with this pair of given names.
Names come and go in popularity (these are called fads), and if your parents have no imagination then you will grow up knowing that you are not unique, because half the people in your classroom will have the same name as yourself. You may even end up being numbered (David #1, David #2, etc). What's worse, if you are not careful then you may end up doing the same thing to your own children.
Indeed, having a common name has only one known advantage — no matter where you go in the world everyone can recognize it, although they may not always spell it and pronounce it the way you expect (David, Davide, Dawit ...). Therefore, you will have no problems making restaurant bookings where ever you happen to be (see Leonard S. Bernstein. 1981. Never Make a Reservation in Your Own Name. Rand McNally).
These days in Australia, "David" struggles to be in the top 100 in popularity for boys. However, currently it appears to be in the top 10 in places like Armenia, Austria, Hungary, Italy, Spain and Israel (in 2012 or 2013), as well as the top 20 in Poland and Portugal. This information comes from The Baby Name Wizard. This site has current lists for many countries (Popular Names From Around the World), but has historical data only for the USA.
So, let's look at the U.S. data in more detail. As for Australia, the peak popularity in the USA was from 1955-1965, as shown in the first graph.
 |
| Note that the peak is truncated from 1950-1960. |
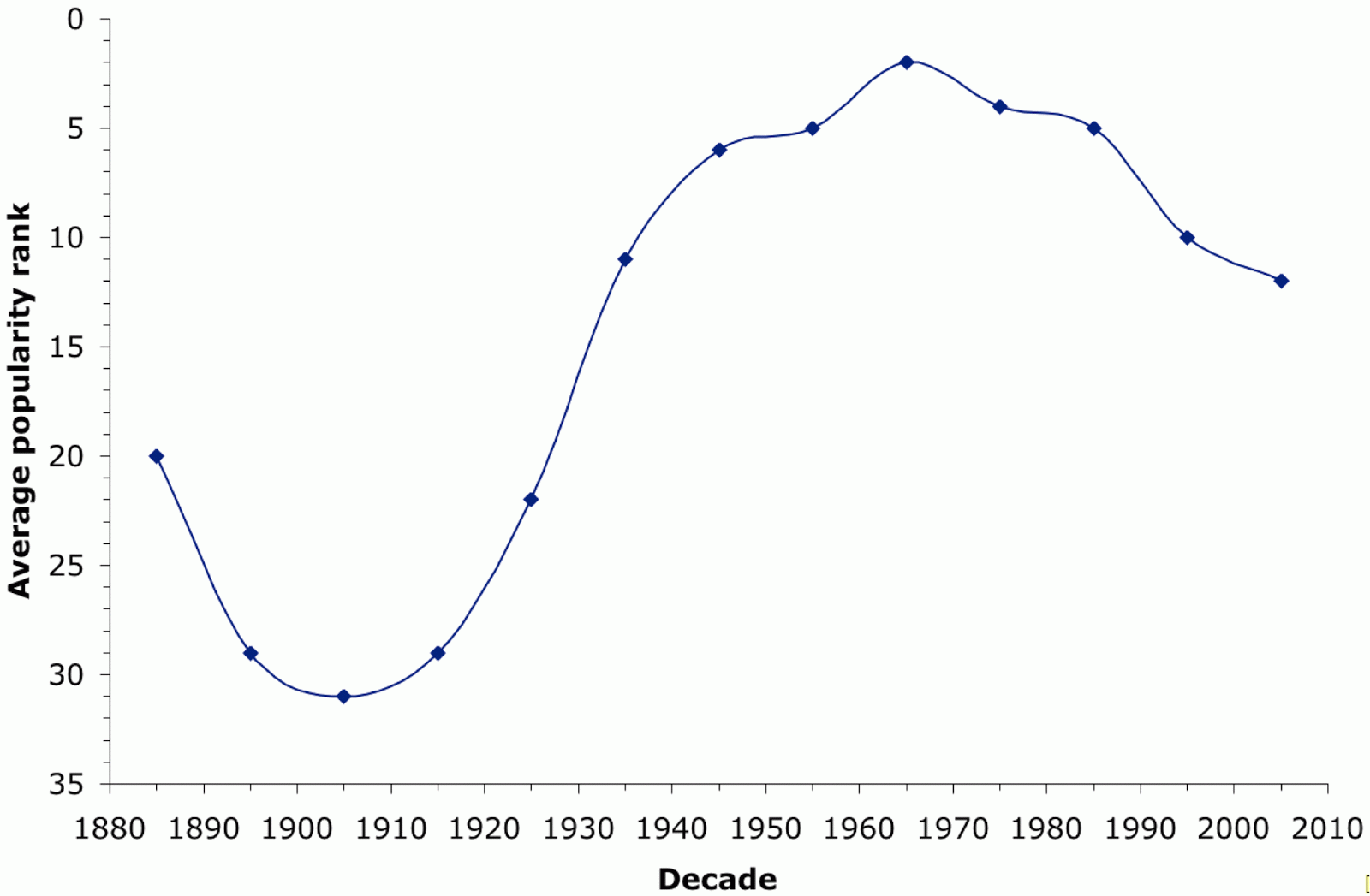
The site's Name Mapper web page has annual data for each state from 1960-2009, which is precisely 50 years. These data show the ranking of names by popularity within each state. The average rank for the name "David" across the 50 states is shown in the next graph. "David" was one of the top 10 names for boys born from 1936-1992, the #1 name in 1960, and it remains inside the top 20 to this day.
We can also look at the data for each state individually, as shown in the next graph, where darker shading represents greater popularity of the name. From the peak in the 1960s there was a steady decrease in almost every state until 1995, after which the popularity has been more erratic. For example, in 1960 "David" was the #1 boys name in 28 of the 50 states (and in the top 5 in every state), but by 1968 it was not #1 anywhere. The last time it was ranked #1 was in Utah in 1970, which was also the last year in which it was in the top 6 in every state.
 |
| Note that the states are grouped and colored geographically / culturallu. |
Only in California and Texas has the name stayed in the top 10 over the past 50 years. In the other states it has stayed in the top 50 or so, except for North Dakota, where it is currently struggling to stay in the top 100. In Nevada and Alaska it has even made a bit of a comeback in the past 10 years.
We can look at the relationship between the states using a phylogenetic network. The next graph is a NeighborNet (based on the manhattan distance) of the 1960-2009 data for the popularity ranking of "David" as a boy's name. States near each other in the network have a similar naming popularity, while states further apart are progressively more different from each other. The network shows a simple trend of increasing average popularity of "David" from the top-left to the bottom-right.
I have also colored the states using the same color scheme as for the previous graph (ie. geographically / culturally). Note that the orange, red, yellow and blue states are fairly neatly grouped, indicating that their alleged geographical / cultural similarity extends to the popularity of given names ("David" has continued to be popular in all of these states). The purple, brown and green states are not grouped very much, indicating much more diversity in the popularity of "David". For example, "David" has continued to be popular in New York and New Jersey but not in Maine, New Hampshire or Vermont. The extreme disinterest of North Dakotans in the name is very clear.
The fall of "David" is not as bad as that of "James" and "John", which were in the top 3 most popular names in the USA all the way from the 1880s to the 1950s, but which are now in 17th and 27th place, respectively (see the timeline graph in the Name Voyager).
I am not sure what has led to the eclipse of these names, other than the whims of faddishness. For example, in Britain and Ireland the name "Harry" has shot to the top in recent years (guess why!), while it still languishes near #700 in the USA. Otherwise, "Noah" and "Liam" seem to have the most widespread popularity for boys in the western world at the moment.
Footnote: I actually got the name Andrew because it is my father's middle name, and his father's before him, and his father's first name.
Wednesday, April 9, 2014
The phylogenetics of angiosperm classification schemes
Alain Cuerrier, Luc Brouillet and Denis Barabe (1998. Numerical and comparative analyses of the modern systems of classification of the flowering plants. Botanical Review 64: 323-355) have provided a genealogy of the various classifications that have been produced for the angiosperms (flowering plants). This is a theoretical construction, intended to express the lines of intellectual influence, either directly expressed by the authors of the classifications, or inferred by comparison of the classifications themselves.
As shown here, it is a classic directed acyclic graph, most of which is tree-like, although some parts are distinctly bushy. Of interest to us, there are also places where hybridizations are indicated.
Cuerrier et al. analyzed the structure of the four modern classifications (by Cronsquist, Dahlgren, Takhtajan, and Thorne) in comparison to their immediate predecessors (by Bessey, Engler, Hallier, and also Gobi). This was a study of affinity relationships, rather than genealogy, and one of their study questions was whether the affinity relationships matched the genealogical ones.
In this regard it is interesting to note that they used clustering and ordination techniques to analyze their quantitative data (comparing the classifications), but they did not use any network techniques. Yet, this would seem to be an obvious strategy, given that they were expecting reticulating relationships.
Unfortunately, none of the datasets shown in the paper is complete, and so I cannot provide a network analysis for them.
The authors summarized their suite of multivariate analyses as an interaction network, as shown next. For each pair of classifications, four statistical tests were performed, and the thickness of the arrows in the network indicates the degree of significant similarity detected: dotted arrow = 2/4 tests show similarity, thin arrow = 3/4 tests, and thick arrow = 4/4 tests.
These semi-quantitative relationships can also be expressed as an unrooted phylogenetic network. I simply took the pairwise similarity scores (0.0, 0.25, 0.5, 0.75, 1.0) and analyzed them using a NeighborNet network. The four modern classifications are highlighted in red.
This more clearly illustrates the various points made by Cuerrier et al. In particular, they note that the intellectual genealogy is not reflected in the affinity relationships of the modern classifications. For example, the Cronquist and Takhtajan classifications are much more similar to that of Hallier than to that of Bessey, whereas Cronquist explicitly cites Bessey as a major influence on his work. Instead, Cronquist's classification is more similar to that of Engler, who does not appear to be genealogically related at all. The distinction between the Thorne and Dahlgren classifications and those of Takhtajan and Cronquist is also obvious.
Labels:
Classification,
EDA
Sunday, April 6, 2014
The sex life of Charles Darwin
Charles Darwin's sex life is of interest because of his consanguineous marriage (to his first cousin), which seems to have resulted in genetic problems for his children, due to inbreeding (see Charles Darwin's family pedigree network). The children of this marriage have recently been discussed in the book by Tim Berra (Darwin and His Children: His Other Legacy). This book discusses Darwin's children mainly in the context of Darwin's own life. Unfortunately, it does not delve much into his personal relationship with either them or his wife, Emma. His private life remains fairly private.
In particular, the book fails to draw any inference from the obvious fact that there were 10 of these children, plus two possible miscarriages. However, obviously we do learn indirectly about a certain part of Mr Darwin's private life. After all, one does not get a woman pregnant accidentally (no matter what your friends try to tell you) -- there are certain biological procedures that you need to go through, and it is fairly difficult to carry these out accidentally. Clearly, Charles and Emma were familiar with this particular activity, and carried it out successfully on numerous occasions.
 |
| Charles Darwin, 2 years before the birth of his last child |
The question is: how many occasions? We know the minimum number, but what about the average rate, for example? The Darwin cottage industry has apparently produced speculations about his sex life before (see Wikipedia), but I have not read about them. Instead, I will provide my own analysis of the situation.
Background
Charles and Emma married on 29 January 1839, when Charles was 29 years and 11 months old and Emma was 30 years and 8 months old. This is pretty late to be starting a family, although not necessarily unusual, and it does have an influence on the calculations.
Emma realized during the following April that she was pregnant (ie. within 3 months); and during the subsequent 18 years she was pregnant a total of 11 more times. On average, there were 500 days between each of the first nine pregnancies, as shown in the first graph. This means that during those 12 years she spent 55% of her days being pregnant and 45% of them not pregnant.
Wikipedia paints an interesting picture of marriages in Victorian Britain (Women in the Victorian era):
When a Victorian man and woman married, the rights of the woman were legally given over to her spouse. Under the law the married couple became one entity where the husband would represent this entity, placing him in control of all property, earnings and money. In addition to losing money and material goods to their husbands, Victorian wives became property to their husbands, giving them rights to what their bodies produced: children, sex and domestic labour. Marriage abrogated a woman's right to consent to sexual intercourse with her husband, giving him 'ownership' over her body. Their mutual matrimonial consent therefore became a contract to give herself to her husband as he desired.The extent to which Emma was involved in the decision to spend more than half of her time pregnant is therefore open to debate. Both her letters and those of her husband do not, as far as I know, reveal any marital difficulties — indeed, quite the contrary. However, Charles' has left us written evidence of his pre-marital ideas about marriage (Darwin’s notes on marriage), which indicate his specific intention to have a family available in his old age.
Note that there are reported to have between two miscarriages between the 9th and 10th births, one in 1852 (when Emma was 44 years old) and one in 1854 (when she was 46). Emma was 48 years and 7 months old when she delivered her final child. Along with the miscarriages, it is worth noting that the final child was born mentally disabled (probably Down's syndrome, for which there is a 1 in 11 chance at age 49), and he died after 18 months. Also, the third child was born after only 36 weeks of pregnancy (instead of the "normal" 40 weeks), and lived for less than a month. Darwin's favorite child was his 2nd (Anne), who unfortunately died of tuberculosis at age 10. The remaining seven children survived to adulthood.
We can also note that the children were born during most periods of the year, as shown in the next graph. However, five of the births were during the 3-month period from early July to late September, implying conception during the period October to December.
In English-speaking countries there is a peak of births in late September, 9 months after the Christmas celebrations (Wellings et al. 1999; Tita et al. 2001). (In Scandinavia, the birth peak is 9 months after the mid-summer celebrations.) Given that two of the births were in this period, we might accuse the Darwins of fitting into this behavioral cliché. However, one of the these two births was the shortened pregnancy, so that conception in that case was on or near to their 3rd wedding anniversary, rather than Christmas. The other conception dates do not fit any pattern that I can see.
All of the above data lead me to the conclusion that most, if not all, of the pregnancies were the result of more-or-less continuously ongoing sexual activity, rather than being the result of deliberate attempts to conceive, or being incidental by-products of celebratory activity. That is, the pregnancies occurred as chance dictated, given the night-time activities being undertaken.
This leads us to the key question of how often these activities took place. We can do some general calculations that might be informative.
Calculation
We now know that the potentially fertile period of human female ovulation is 12 days out of every 28, and vaginal sex during this period should be avoided if you do not wish to be involved in a pregnancy (Arévalo et al. 1999). Within this window of opportunity there is a 6-day period during which conception is most likely (Dunson et al. 2002; Stirnemann et al. 2013), and if you are trying to conceive a child then sex at least twice during this period is the recommended strategy. (Each egg lasts 1 day, but sperm last for 3 days, so that sex more than 2-3 times doesn't seem to improve your chances.) Clearly, sex once during this 6-day period is a reasonable minimum expectation for conception.
However, the probability of conception even under these minimum circumstances is very dependent on the age of the female involved. (The eggs are produced early in the female's life, and the eggs age along with the woman, so that older eggs have reduced fertility; Broekmans et al. 2009.) For example (Siebler 2009; Sozou & Hartshorne 2012), in her early 20s a healthy fertile woman has a 20–25% probability of conception each month. The average time to achieve conception for this age group is 4 months, and the likelihood of conception within one year is 93–97%. More importantly, in her early 30s (as Emma was when she married) the probability of conception each month drops to 10–15%, so that the average time of conception is 10 months and the likelihood of conception within one year is c.72%. The probability keeps dropping until menopause (where it reaches zero), so that, for example, the likelihood of conception within one year is c.65% for a woman in her late 30s.
 |
| Emma, near the time of her marriage |
This means that, given her age, Emma had to receive sperm during every ovulation cycle, in order to maintain a 50% chance of getting pregnant within any one year (she got pregnant on average every 9-12 months). If you know the ovulation times, then that rate requires sex 13 times per year. If you don't know the times, or you don't know anything about ovulation cycles (and it seems likely that Victorian women did not), then it requires sex at least once per week in order to hit them all by random chance.
So, I arrive at the conclusion of weekly sex for the Darwins throughout the first 12 years of their marriage, and possibly for 18 years. Calculations seem to be much more difficult after that, due to lack of suitable data.
I have no idea whether this weekly rate was normal for Victorian couples, but it certainly seems to be quite normal in the modern world, for people of their age. As shown in the next graph, people in their 30s and 40s currently report having sex every 4-5 days throughout the year (Mosher et al. 2005; Schneidewind-Skibbe et al. 2008). So, Charles' sex life would fit perfectly into the 21st century.
 |
| From Mosher et al. (2005) |
Postscript
Finally, it is interesting to note that Charles started writing what he called his "Big Species Book" shortly after the birth of his final child. Furthermore, he converted this incomplete manuscript into what is now known as On the Origin of Species after the early death of that same child. Other events were involved in these decisions, of course, but his changing family life is unlikely to have been the least important of them.
References
Arévalo M, Sinai I, Jennings V (1999) A fixed formula to define the fertile window of the menstrual cycle as the basis of a simple method of natural family planning. Contraception 60: 357-360.
Broekmans FJ, Soules MR, Fauser BC (2009) Ovarian aging: mechanisms and clinical consequences. Endocrine Reviews 30: 465-493.
Dunson DB, Colombo B, Baird DD (2002) Changes with age in the level and duration of fertility in the menstrual cycle. Human Reproduction 17: 1399-1403.
Mosher WD, Chandra A, Jones J (2005) Sexual behavior and selected health measures: men and women 15–44 years of age, United States, 2002. Advance Data From Vital and Health Statistics 362. National Center for Health Statistics, Hyattsville, MD.
Schneidewind-Skibbe A, Hayes RD, Koochaki PE, Meyer J, Dennerstein L (2008) The frequency of sexual intercourse reported by women: a review of community-based studies and factors limiting their conclusions. Journal of Sexual Medicine 5: 301-335.
Siebler SJ (2009) How to Get Pregnant. Little, Brown and Co, New York, NY.
Sozou PD, Hartshorne GM (2012) Time to pregnancy: a computational method for using the duration of non-conception for predicting conception. PLoS One 7: e46544.
Stirnemann JJ, Samson A, Bernard JP, Thalabard JC (2013) Day-specific probabilities of conception in fertile cycles resulting in spontaneous pregnancies. Human Reproduction 28: 1110-1116.
Tita AT, Hollier LM, Waller DK (2001) Seasonality in conception of births and influence on late initiation of prenatal care. Obstetrics & Gynecology 97: 976-981.
Wellings K, Macdowall W, Catchpole M, Goodrich J (1999) Seasonal variations in sexual activity and their implications for sexual health promotion. Journal of the Royal Society of Medicine 92: 60-64.
Labels:
Darwin
Tuesday, April 1, 2014
April fools and phylogeneticists
Today is All Fool's Day. The tradition apparently started in the Netherlands and northern Germany, where on April 1 people would be sent on a long series of purposeless errands, and thus be made to feel increasingly foolish as the day went on. (This is now known as "a wild goose chase".) The Museum of Hoaxes has a detailed history (The Origin of April Fool’s Day), plus supplementary information about a Dutch poem from 1561 and the first German reference in 1618.
This tradition has been modified in the past 150 years or so, to one where outrageous stories are told, usually in public, to see how many people can be made to believe that they are true. The media are often involved, particularly newspapers and television shows. These "hoaxes" are usually revealed by the end of the day — indeed, if they continue, then they are usually referred to as hoaxes rather than as April fool jokes.
The Museum of Hoaxes has a compilation of what the curator believes to be the Top 100 April Fool's Day Hoaxes of All Time, which makes interesting reading.
Phylogenetics and evolutionary biology are not immune from these activities, of course. I have listed here a few of the jokes perpetrated in recent years on the internet, just in case nothing much happened today and you want to read about something appropriate anyway.
Tetrapod Zoology (April 1 2011)
Science meets the Mokele-Mbembe!
Molecular Phylogenetics and Evolution (April 1 2004)
Molecular phylogenetic analysis of mtDNA sequences from the Yeti
Raptormaniac (April 1 2013)
Hail Volantia
Tetrapod Zoology (April 1 2013)
Welcome to the Squamozoic!
Shit You Didn't Know About Biology (April 1 2012)
Dragons
The Tree of Life (April 1 2008)
Confessions of an April Fool, and the dope on brain doping
Evolving Thoughts (April 1 2009)
New work on lateral transfer shows that Darwin was wrong
The Genealogical World of Phylogenetic Networks (April 1 2013)
Empedocles, Lucretius and lateral gene transfer
Computational Footnote
There are plenty of computational jokes in the world, mostly involving unsuccessful mathematical proofs, but none of them seem to have much to do with phylogenetics. Is there a message here? For example, physicists, ever the pranksters, typically use the arXiv pre-print repository to post spurious papers on April 1, with some examples noted at MetaFilter for April 2012 (April Fools for physicists).
Labels:
History
Subscribe to:
Posts (Atom)