Monday, August 26, 2019
Statistical proof of language relatedness (Open problems in computational diversity linguistics 7)
The more I advance with the problems I want to present during this year, the more I have to admit to myself, sometimes, that the problem I planned to present is so difficult that I find it even hard to simply present the state-of-the-art. The problem of this month, problem number 7 in my list, is such an example — proving that two or more languages are "genetically related", as historical linguists (incorrectly) tend to say, is not only hard, it is also extremely difficult even to summarize the topic properly.
Typically, colleagues start with the famous but also not very helpful quote of Sir William Jones, who delivered a report to the British Indian Company, thereby mentioning that there might be a deeper relationship between Sanskrit and some European languages (like Greek and Latin). The article, titled The third anniversary discourse, delivered 2 February, 1786, by the president (published in 1798) has by now been quoted so many times that it is better to avoid quoting it another time (but you will find the full quote with references in my reference library.
In contrast to later scholars like Jacob Grimm and Rasmus Rask, however, Jones does not prove anything, he just states an opinion. The reason why scholars like to quote him, is that he seems to talk about probability, since he mentions the impossibility that the resemblances between the languages he observed could have arisen by chance. Since a great deal of the discussion about language relationship centers around the question how chance could be controlled for, it is a welcome quote from the olden times to be used when writing a paper on statistics or quantitative methods. But this does not necessarily mean that Jones really knew what he was writing about, as one can read in detail in the very interesting book by Campbell and Poser (2008), which deals at length with the supposedly overrated role that William Jones played in the early history of historical linguistics.
Macro Families
Returning to the topic at hand. The regularity of sound change and the possibility to prove language relationship in some cases was an unexpected detection of some linguists during the early 19th century, but what many linguists have been dreaming about since is to expand their methods to such a degree that even deeper relationships could be proven. While the evidence for the relationship of the core Indo-European languages was more or less convincing by itself (as rightfully pointed out by Nichols 1996), scholars have proposed many suggestions of relationship, many of which are no longer followed by the communis opinio. Among these long-range proposals for deep phylogenetic relations are theories that further unite fully established language families, proposing large macro-families — such as Nostratic (uniting Semitic, Indo-European, and many more, depending on the respective version), Altaic (uniting Turkic, Mongolic, Tungusic, Japanese, and Korean, etc.), or Dene-Caucasian (uniting Sino-Tibetan, North Caucasian, and Na-Dene), which span incredibly large areas on earth.
Given that it the majority of scholars mistrust these new and risky proposals, and that even scholars who work in the field of long-range comparison often disagree with each other, it is not surprising that at least some linguists became interested in the question of how long-range relationship could be proven in the end. One of the first attempts in this regard was presented by Aharon Dolgopolsky, a convinced Nostratic linguist, who presented a first, very interesting, heuristic procedure to determine deep cognates and deep language relationships, by breaking sounds down to more abstract classes, in order to address the problem that words often do no longer look similar due to sound change (Dolgopolsky 1964).
Why it is hard to prove language relationship
Dolgopolsky did not use any statistics to prove his approach, but he emphasized the probabilistic aspect of his endeavor, and derived his "consonant classes" or "sound classes" as well as his very short list of stable concepts from the empirical investigation of a large corpus. The core of his approach, to fix a list of semantic items, presumably "stable" (i.e. slowly changing with respect to semantic shift), and to reduce the complexity of phonetic transcriptions to a core meta-alphabet, has been the basis of many follow-up studies that follow an explicitly quantitative (or statistic) approach.
As of now, most scholars, be they classical or computational, agree that the first stage of historical language comparison consists of the proof that the languages one wants to investigate are, indeed, historically related to each other (for the underlying workflow of historical language comparison, see Ross and Durie). In a blogpost published much earlier (Monogenesis, polygenesis, and militant agnosticism I have already pointed to this problem, as it is quite different from biology, where independent evolution of life is usually not assumed by scholars, while linguistic research can never really exclude it.
While proving language relationship of closely related languages is often a complete no-brainer, it becomes especially then hard, when exceeding some critical time depth. Where this time depth lies is not clear by now, but based on our observations regarding the paste in which languages replace existing words with new ones, borrow words, or loose and build grammatical structures, it is clear that it is theoretically possible that a language group could have lost all hints on its ancestry after 5,000 to 10,000 years. Luckily, what is theoretically possible for one language, does not necessarily happen with all languages in a given sample, and as a result, we find still enough signal for ancestral languages in quite a few language families of the world, that allows us to draw conclusions that go back about 10,000 years in the most cases, if not even deeper in some cases.
Traditional insights into the proof of language relationships
The difficulty of the task is probably obvious without further explanation — the more material a language acquires from its neighbors, and the more it loses or modifies the material it inherited from its ancestors, the more difficult it is for the experts to find the evidence that convinces their colleagues about the phylogenetic affiliation of such a language. While regular sound changes can easily convince people of phylogenetic relationship, the evidence that scholars propose for deeper linguistic groupings is rarely large enough to establish correspondences.
As a result, scholars often resort to other types of evidence, such as certain grammatical peculiarities, certain similarities in the pronunciation of certain words, or external findings (e.g.,from archaeology). As Handel (2008) points out, for example, a good indicator of a Sino-Tibetan language is that its words for five, I, and fish start with similar initial sounds and contain a similar vowel (compare Chinese wǔ, wǒ, and yú, going back to MC readings ŋjuX. ŋaX, and ŋjo). While these arguments are often intuitively very convincing (and may also be statistically convincing, as Nichols 1996 argues), this kind of evidence, as mentioned by Handel, is extremely difficult to detect, since the commonalities can be found in so many different regions of a human language system.
While linguists also use sound correspondences to prove and establish relationship, there are no convincing cases known to me in which sound correspondences were employed to prove relationships beyond a certain time depth. One can compare this endeavor to some degree with the work of police commissars who have to find a murderer, and can do so easily if the person responsible left DNA at the spot, while they have to spend many nights in pubs, drinking cheap beer and smoking bad cigarettes, in order to wait for the spark of inspiration that delivers the ultimate proof not based on DNA.
Computational and statistical approaches
Up to now, no computational methods are available to find signals of the kind presented by Handel for Sino-Tibetan, i.e, a general-purpose heuristic to search for what Nichols (1996) calls individual-identifying evidence. So,computational and statistical methods have so far been based on very schematic approaches, which are almost exclusively based on wordlists. A wordlist can hereby be thought of as a simple table with a certain number of concepts (arm, hand, stone, cinema) in the first column, and translation equivalents for these concepts being listed for several different languages in the following columns (see List 2014: 22-24). This format can of course be enhanced (Forkel et al. 2018), but it represents the standard way in which many historical linguists still prepare and curate their data.
What scholars now try to do is to see if they can find some kind of signal in the data that they think would be unlikely to be detected by chance. In general, there are two ways that scholars have explored so far. In the approach proposed by Ringe (1992), the signalsthat are tested for in the wordlists are sound correspondences, and we can therefore call theses approaches correspondence-based approaches to prove language relationship. In the approach of Baxter and Manaster Ramer (2000), which follows the original idea of Dolgopolsky, the data are converted to sound classes first, and cognacy is assumed for words with identical sound classes. Sound-class-based approaches again try to illustrate that the matches that can be identified are unlikely to be due to chance.
Both approaches have been discussed in quite a range of different papers, and scholars have also tried to propose improvements to the methods. Ringe's correspondence-based approach showed that it can become difficult to prove the relationship of languages formally, although we have very good reasons to assume it based on our standard methods. Baxter and Manaster Ramer (2000) presented a more optimistic case study, in which they argue that their sound-class-based approach would allow them to argue in favor of the relationship of Hindi and English, even if the two languages are separated by at least 10,000 or even more years.
A general problem of Ringe's approach was that he tried to use combinatorics to arrive at his statistical evaluation. This is similar to the way in which Henikoff and Henikoff (1992) developed their BLOSUM matrices for biology, by assuming that the only factor that handles the combination of amino acids in biological sequences is their frequency. Ringe tried to estimate the likelihood of finding matches of word-initial consonants in his data by using a combinatorial approach based on the assumption of simple sound frequencies in the word lists he investigated. The general problem with linguistic sequences, however, is that they are not randomly arranged. Instead, every language has its own system of phonotactic rules, a rather simple grammar that restricts certain letter combinations and favors others. All spoken languages have these systems, and some vary greatly with respect to their phonotactics. As a result, due to the inherent structure of sequences, a bag of symbols approach, as used by Ringe, can have unwanted side effects and invoke misleading estimates regarding the probability of certain matches.
To avoid this problem, Kessler (2001) proposed the use of permutation tests, by which the random distribution, against which the attested distribution is compared, is generated via the shuffling of the lists. Instead of comparing translations for "apple" in one language with translations for "apple" in another language, one compares now translations for pear with translations for "apple", hoping that this — if done often enough — better approximates the random distribution (i.e. the situation in which one compares several known unrelated languages with similar phoneme inventories).
Permutation is also the standard in all sound-correspondence-based approaches. In a recent paper, Kassian et al. (2015) used these approaches (first proposed by Turchin et al. 2010) to argue for the relationship of Indo-European and Uralic languages by comparing reconstructed word lists for Proto-Indo-European and Proto-Uralic. As can be seen from the discussion of these findings involving multiple authors, people are still not automatically convinced by a significance test, and scholars have criticized: their choice of test concepts (they used the classical 110-item list by Yakhontov and Starostin), their choice of reconstruction system (they did not use the mysterious laryngeals in their comparison), and the possibility that the findings were due to other factors (early borrowing).
While there have been some more attempts to improve the correspondence-based and the sound-class-based approaches (e.g., Kessler 2007, Kilani 2015, Mortarino 2009), it is unlikely that they will lead to the consolidation of contested proposals on macro families any time soon. Apart from the general problems of many of the current tests, there seem to be too many unknowns that prevent the community to accept findings, no matter "how" significant they appear. As can be nicely seen from the reaction to the paper by Kassian et al. 2015, a significant test will first raise the typical questions regarding the quality of the data and the initial judgments (which may also at times be biased). Even if all scholars would agree in this case, however, i.e. if one could not criticize anything in the initial test setting, there would still be the possibility to say that the findings reflect early language contact instead of phylogenetic relatedness.
Initial ideas for improvement
What I find unsatisfying about most existing tests is that they do not make exhaustive use of alignment methods. The sound-class-based approach is a shortcut for alignments, but it reduces words to two consonant classes only, and requires an extensive analysis of the words to compare only the root morpheme. It therefore also opens the possibility to bias the results (even if scholars may not intend that directly). While correspondence-based tests are much more elegant in general, they avoid alignments completely, and just pick the first letter in every word. The problem seems to be that — even when using permutations to generate the random distribution — nobody really knows how one should score the significance of sound correspondences in aligned words. I have to admit that I do not know it either. Although the tools for automated sequence comparison that my colleagues and I have been developing in the past (List 2014, List et al. 2018) seem like the best starting point to improve the correspondence-based approach, it is not clear how the test should be performed in the end.
Additionally, I assume also that expanded, fully fledged, tests will ultimately show what I reported back in my dissertation — if we work on limited wordlists, with only 200 items per language, the test will drastically lose its power when certain time depths have been reached. While we can easily prove the relationship of English and German, even with only 100 words, we have a hard time doing the same thing for English and Albanian (see List 2014: 200-203). But expanding the wordlists bears another risk for comparison (as pointed out to me by George Starostin): the more words we add, the more likely it is that they have been borrowed. Thus, we face a general dilemma in historical linguistics: that we are forced to deal with sparse data, since languages tend to lose their historical signal rather quickly.
Outlook
While there is no doubt that it would be attractive to have a test that would immediately tell one whether languages are related or not, I am becoming more and more skeptical about whether this test would actually help us, specifically when concentrating on pairwise tests alone. The challenge of this problem is not just to design a test that makes sense and does not overly simplify. The challenge is to propagate the test in such a way that it convinces our colleagues that it really works. This, however, is a challenge that is greater than any of the other open problems I have discussed so far in this year.
References
Baxter, William H. and Manaster Ramer, Alexis (2000) Beyond lumping and splitting: Probabilistic issues in historical linguistics. In: Renfrew, Colin and McMahon, April and Trask, Larry (eds.) Time Depth in Historical Linguistics. Cambridge:McDonald Institute for Archaeological Research, pp. 167-188.
Campbell, Lyle and Poser, William John (2008) Language Classification: History and Method. Cambridge:Cambridge University Press.
Dolgopolsky, Aron B. (1964) Gipoteza drevnejšego rodstva jazykovych semej Severnoj Evrazii s verojatnostej točky zrenija [A probabilistic hypothesis concering the oldest relationships among the language families of Northern Eurasia]. Voprosy Jazykoznanija 2: 53-63.
Forkel, Robert and List, Johann-Mattis and Greenhill, Simon J. and Rzymski, Christoph and Bank, Sebastian and Cysouw, Michael and Hammarström, Harald and Haspelmath, Martin and Kaiping, Gereon A. and Gray, Russell D. (2018) Cross-linguistic data formats, advancing data sharing and re-use in comparative linguistics. Scientific Data 5: 1-10.
Handel, Zev (2008) What is Sino-Tibetan? Snapshot of a field and a language family in flux. Language and Linguistics Compass 2: 422-441.
Henikoff, Steven and Henikoff, Jorja G. (1992) Amino acid substitution matrices from protein blocks. Proceedings of the National Academy of Sciences 89: 10915-10919.
Jones, William (1798) The third anniversary discourse, delivered 2 February, 1786, by the president. On the Hindus. Asiatick Researches 1: 415-43.
Kassian, Alexei and Zhivlov, Mikhail and Starostin, George S. (2015) Proto-Indo-European-Uralic comparison from the probabilistic point of view. The Journal of Indo-European Studies 43: 301-347.
Kessler, Brett (2001) The Significance of Word Lists. Statistical Tests for Investigating Historical Connections Between Languages. Stanford: CSLI Publications.
Kessler, Brett (2007) Word similarity metrics and multilateral comparison. In: Proceedings of Ninth Meeting of the ACL Special Interest Group in Computational Morphology and Phonology, pp. 6-14.
Kilani, Marwan (2015): Calculating false cognates: An extension of the Baxter & Manaster-Ramer solution and its application to the case of Pre-Greek. Diachronica 32: 331-364.
List, Johann-Mattis (2014) Sequence Comparison in Historical Linguistics. Düsseldorf: Düsseldorf University Press.
List, Johann-Mattis and Walworth, Mary and Greenhill, Simon J. and Tresoldi, Tiago and Forkel, Robert (2018) Sequence comparison in computational historical linguistics. Journal of Language Evolution 3: 130–144.
Mortarino, Cinzia (2009) An improved statistical test for historical linguistics. Statistical Methods and Applications 18: 193-204.
Nichols, Johanna (1996) The comparative method as heuristic. In: Durie, Mark (ed.) The Comparative Method Reviewed. New York:Oxford University Press, pp. 39-71.
Ringe, Donald A. (1992) On calculating the factor of chance in language comparison. Transactions of the American Philosophical Society 82: 1-110.
Ross, Malcolm D. (1996) Contact-induced change and the comparative method. Cases from Papua New Guinea. In: Durie, Mark (ed.) The Comparative Method Reviewed. New York: Oxford University Press, pp. 180-217.
Turchin, Peter and Peiros, Ilja and Gell-Mann, Murray (2010) Analyzing genetic connections between languages by matching consonant classes. Journal of Language Relationship 3: 117-126.
Monday, August 19, 2019
Phylogenetics of chain letters?
The general public and the general media often have no idea what biologists mean by the work "evolution". The word has two possible meanings, and they usually pick the wrong one. Niles Eldredge tried to clarify the situation by referring to them:
- transformational evolution — the change in a group of objects resulting from a change in each object (often attributed to Lamarck)
- variational evolution - the change in a group of objects resulting from a change in the proportion of different types of objects (usually attributed to Darwin).
So, it was with some trepidation that I looked at an article in Scientific American called Chain letters and evolutionary histories (by Charles H. Bennett, Ming Li and Bin Ma. June 2003, pp. 76-81). It was subtitled: "A study of chain letters shows how to infer the family tree of anything that evolves over time, from biological genomes to languages to plagiarized schoolwork."
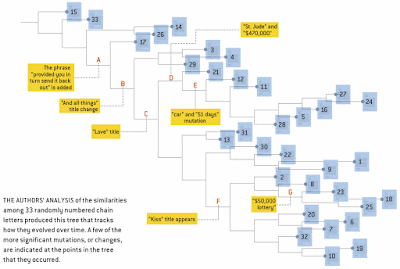
The "taxa" in their study consist of 33 different chain letters, collected during the period 1980–1995 (8 other letters were excluded), covering the diversity of chain letters as they existed before internet spam became widespread. These letters can be viewed on the Chain Letters Home Page.
The main issue with this study is that there are no clearly defined characters, from which the phylogeny could be constructed. The authors therefore resort to creating a pairwise distance matrix, among the taxa, in a manner (compression) that I have criticized before (Non-model distances in phylogenetics). I have also discussed previous examples where this approach has been used, notably: Phylogenetics of computer viruses? Multimedia phylogeny?
The essential problem, as I see it, is that without a model of character change there is no reliable way to separate phylogenetic information from any other type of information. That is, phylogenetic similarity is a special type of similarity. It is based on the idea of shared derived character states, as these are the only things that are informative about a phylogeny.
Compression, on the other hand, is a general sort of similarity, based on the idea of information complexity. This presumably will contain some useful phylogenetic information, but it will also contain a lot of irrelevance — for example, shared ancestral character states, which are uninformative at best and positively misleading at worst.
So, the authors can easily produce an unrooted tree from their similarity matrix, which they then proceed to root at one of the letters that they collected early on in their study. This tree is shown here.
However, whether this diagram represents a phylogeny is unknown.
Nevertheless, that does not stop us using an unrooted phylogenetic network as a form of exploratory data analysis, as we have done so often in this blog. This is not intended to produce a rooted evolutionary history, but instead merely to summarize the multivariate information in a comprehensible (and informative) manner. This might indicate whether we are likely to be able to reconstruct the phylogeny In this case, I have used a NeighborNet to display the similarity matrix, as shown next.
It is easy to see that the relationships among the letters are not particularly tree-like. Moreover, the long terminal edges emphasize that much of the complexity information is not shared among the letters, while the shard information is distinctly net-like. So, a simple "phylogenetic tree" (as shown above) is not likely to be representative of the actual evolutionary history.
However, there are actually a few reasonably well-defined groups among the taxa — one at the top. one at the right, and several at the bottom of the network. There are also letters of uncertain affinity, such as L2, L23, L13 and L31. These may reflect phylogenetic history, even though that history is hard to untangle.
Finally, it is worth noting that the history of chain letters, dating back to the 1800s, is discussed in detail by Daniel W. VanArsdale at his Chain Letter Evolution web pages.
Labels:
Exploratory data analysis
Monday, August 12, 2019
Public transit trips in the USA
Public transport, or mass transit, has long been a politically charged issue, throughout the world. However, the modern world now recognizes that it is an effective way to deal with mass movements of people in a manner that respects the use of non-renewable resources.
After all, the only way to continue with autonomous transportation is to get rid of fossil fuels. However. electric cars will not be of much use until we work out where we are going to get all of the needed extra electricity, in a manner that is environmentally friendly. There is not much point in simply moving the burning of fossil fuels from the vehicle (ie. gasoline) to a power station that also burns fossil fuels (eg. coal). There is also a limit to how many rivers there are left to dam for hydroelectric power; and nuclear reactors have gone out of fashion (fortunately). There is also, of course, the matter of how we are going to recycle the used (lithium-ion) batteries from the cars, which is apparently a tougher proposition than recycling the electric motors themselves.
So, until we sort this out, mass transit is a viable option for most conurbations. In this context, a conurbation (or a metropolitan area) is a contiguous area within which large numbers of people move regularly, especially traveling to and from their workplace each weekday. A conurbation often involves multiple cities and towns, as defined by political administrations or contiguous urban development — many people live in one urban area but work in another.
So, naturally, governments collect data on these matters. One such data collection is the U.S. Department of Transportation's National Transit Database. The data consist of "sums of annual ridership (in terms of unlinked passenger trips), as reported by transit agencies to the Federal Transit Administration." Data for three separate modes of transit are included: bus, rail, and paratransit. The data currently cover the years 2002–2018, inclusive.
To look at the data for the 42 U.S. conurbations included, for the year 2018, I have performed this blog's usual exploratory data analysis. I first calculated the transit rate per person, by dividing the annual number of trips for each of the three modes by the conurbation population size. Since these are multivariate data, one of the simplest ways to get a pictorial overview of the data patterns is to use a phylogenetic network. For this network analysis, I calculated the similarity of the conurbations using the manhattan distance. A Neighbor-net analysis was then used to display the between-area similarities.
The resulting network is shown in the graph. Conurbations that are closely connected in the network are similar to each other based on the trip rates, and those areas that are further apart are progressively more different from each other. In this case, there is a simple gradient from the busiest mass transit systems at the top of the network to the least busy at the bottom.
The network shows us that the New York – Newark transit-commuting area (which covers part of three states) is far and away the busiest in the USA. The subway system dominates this mass transit, of course, as it is justifiably world famous, although not always for the best of reasons as far as commuters are concerned
The San Francisco – Oakland area is in clear second place. Here, bus transit slightly exceeds rail transit. Then follows Washington DC and Boston, both of which also cover parts of three states. In Boston trains out-do buses 2:1, while in Washington it is closer to 1.5:1.
Nest comes a group of four conurbations: Chicago, Philadelphia, Portland and Seattle. Two of these cover part of Washington, but in quite different ways — in Seattle the buses dominate the system 5:1 but in Portland it is only 1.5:1. Chicago and Philadelphia share buses and trains pretty equally.
At the bottom of the network there are two large groups of conurbations, one of which does slightly better than the other at mass transit use. The least-used system is that of San Juan, in Puerto Rico, perhaps not unexpectedly. Of the contiguous U.S. states, Indianapolis (IN) has the least used system, followed by Memphis (TN–MS–AR).
Moving on, we could also look at changes in the total number of transit trips (irrespective of mode) during the period for which data are available: 2002–2018. A network is of little help here. So, it so simplest just to plot the data, as shown in the next graph.
For most of the metropolitan areas there is little in the way of consistent change through time. However, there are some areas that show high correlations between the number of trips and time. These are the areas that have shown the most consistent increase in the number of transit trips from 2002–2018:
- Chicago (IL–IN)
- Tampa – St Petersburg (FL)
- Baltimore (MD)
- Denver – Aurora (CO)
- San Francisco – Oakland (CA)
- Memphis (TN–MS–AR)
- San Diego (CA)
- Cleveland (OH)
- Providence (RI–MA)
- Orlando (FL)
- Indianapolis (IN)
- New York – Newark (NY–NJ–CT)
- Portland (OR–WA)
- Minneapolis – St Paul (MN–WI)
- Kansas City (MO–KS)
- Columbus (OH)
- Riverside – San Bernardino (CA)
Declining transit numbers is a topic discussed around the web; for example: Transit ridership down in most American cities. This article has a graph neatly showing the change in transit numbers from 2017 to 2018. It shows marked decreases, particularly for bus trips, while the few increases almost all involved rail travel. Is this a short-term effect, or the start of a general long-term decline?
Monday, August 5, 2019
Tattoo Monday XIX
Here are two more (large) Charles Darwin tree tattoos, based on his best-known sketch from his Notebooks (the "I think" tree). For other examples, see Tattoo Monday III, Tattoo Monday V, Tattoo Monday VI, Tattoo Monday IX, Tattoo Monday XII, and Tattoo Monday XVIII.
Labels:
Tattoo
Subscribe to:
Posts (Atom)