The fifth problem in my list of open problems in computational diversity linguistics is devoted to the problem of simulating lexical change. In a broad sense, lexical change refers to the way in which the lexicon of a human language evolves over time. In a narrower sense, we would reduce it to the major processes that constitute the changes that affect the words of human languages.
Following Gevaudán (2007: 15-17), we can distinguish three different dimensions along which words can change, namely:
- the semantic dimension — a given word can change its meaning
- the morphological dimension —new words are formed from old words by combining existing words or deriving new words with help of affixes, and
- the stratic dimension — languages may acquire words from their neighbors and thus contain strata of contact.
Create a model of lexical change that simulates how the lexicon of a given language changes over time. This model may be simplifying, but it should account for change along the major dimensions of lexical change, including morphological change, semantic change, and lexical borrowing.Note that the focus on three dimensions along which a word can change deliberately excludes sound change (which I will treat as a separate problem in an upcoming blogpost). Excluding sound change is justified by the fact that, in the majority of cases, the process proceeds independently from semantic change, morphological change, and borrowing, while the latter three process often interact.
There are, of course, cases where sound change may trigger the other three processes — for example, in cases where sound change leads to homophonous words in a language that express contrary meanings, which is usually resolved by using another word form for one of the concepts. An example for this process can be found in Chinese, where shǒu (in modern pronunciation) came to mean both "head" and "hand" (spelled as 首 and 手). Nowadays, shǒu remains only in expressions like shǒudū 首都 "capital", while tóu 头 is the regular word for "head".
Since the number of these processes where we have sufficient evidence to infer that sound change triggered other changes is rather small, we will do better to ignore it when trying to design initial models of lexical change. Later models could, of course, combine sound change with lexical change in an overarching framework, but given how the modeling of lexical change is already complex just with the three dimensions alone, it seems useful to put it aside for the moment and treat it as a separate problem.
Why simulating lexical change is hard
For historical linguists, it is obvious why it is hard to simulate lexical change in a computational model. The reason is that all three major processes of lexical change, semantic change, morphological change, and lexical borrowing, are already hard to model and understand themselves.
Morphological change is not only difficult to understand as a process, it is even difficult to infer; and it is for this reason, that we find morphological segmentation as the first example in my list of open problems. The same holds for lexical borrowing, which I discussed as the second example in my list of open problems. The problem of common pathways of semantic change will be discussed in a later post, devoted to the general typology of semantic change processes.
If each of the individual processes that constitute lexical change is itself either hard to model or to infer, it is no wonder that the simulation is also hard.
Traditional insights into the process of lexical change
Important work on lexical change goes back at least to the 1950s, when Morris Swadesh (1909-1967) proposed his theory of lexicostatistics and glottochronology (Swadesh 1952, 1955, Lees 1953). What was important in this context was not the idea that one could compute the divergence time of languages, but the data model which Swadesh introduced. This data model is represented by a word-list in which a particular list of concepts is translated into a particular range of languages. While former work on semantic change had been mostly onomasiological — ie. form-based, taking the word as the basic unit and asking how it would change its meaning over time — the new model used concepts as a comparandum, investigating how word forms replaced each other in expressing specific contexts over time. This onomasiological or concept-based perspective has the great advantage of drastically facilitating the sampling of language data from different languages.
When comparing only specific word forms for cognacy, it is difficult to learn something about the dynamics of lexical change through time, since it is never clear how to sample those words that one wants to investigate more closely in a given study. With Swadesh's data model, the sampling process is reduced to the selection of concepts, regardless of whether one knows how many concepts one can find in a given sample of languages. Swadesh was by no means the first to propose this perspective, but he was the one who promulgated it.
Swadesh's data model does not directly measure lexical change, but instead measures the results of lexical change, given that its results surface in the distribution of cognate sets across lexicostatistical word-lists. While historical linguists mostly focused on sound change processes before, often ignoring morphological and semantic change, the lexicostatistical data model moved semantic change, lexical borrowing, and (to a lesser degree also) morphological change into the spotlight of linguistic endeavors. As an example, consider the following quote from Lees (1953), discussing the investigation of change in vocabulary under the label of morpheme decay:
The reasons for morpheme decay, ie. for change in vocabulary, have been classified by many authors; they include such processes as word tabu, phonemic confusion of etymologically distinct items close in meaning, change in material culture with loss of obsolete terms, rise of witty terms or slang, adoption of prestige forms from a superstratum language, and various gradual semantic shifts such as specialization, generalization, and pejoration. [Lees 1953: 114]In addition to lexicostatistics and the discussions that arose especially from it (including those that criticized the method harshly), I consider the aforementioned model of three dimensions of lexical change by Gevaudán (2007) to be very useful in this context, since it constitutes one of the few attempts to approach the question of lexical change in a formal (or formalizable) way.
Computational approaches
Among the most frequently used models in the historical linguistics literature are those in which lexical change is modeled as a process of cognate gain and cognate loss. Modeling lexical change as a process of word gain and word loss, or root gain and root loss, is in fact straightforward. We well know that languages may cease to use certain words during their evolution, either because the things the words denote no longer exist (think of the word walkman and then try to project the future of the word ipad), or because a specific word form is no longer being used to denote a concept and therefore drops out of the language at some point (think of thorp which meant something like "village", as a comparison with German Dorf "village" shows, but now exists only as a suffix in place names).
Since the gain-loss (or birth-death) model finds a direct counterpart in evolutionary biology, where genome evolution is often modeled as a process involving gain and loss of gene families (Cohen et al. 2008), it is also very easy to apply it to linguistics. The major work on the stochastic description of different gain-loss models has already been done, and we can find very stable software to helps us employ gain-loss models to reconstruct phylogenetic trees (Ronquist and Huelsenbeck 2003).
It is therefore not surprising that gain-loss models are very popular in computational approaches to historical linguistics. Starting from pioneering work by Gray and Jordan (2000) and Gray and Atkinson (2003), they have now been used on many language families, including Austronesian (Gray et al. 2007), Australian languages (Bowern and Atkinson 2012), and most recently also Sino-Tibetan (Sagart et al. 2019). Although scholars (including myself) have expressed skepticism about their usefulness (List 2016), the gain-loss model can be seen as reflecting the quasi-standard of phylogenetic reconstruction in contemporary quantitative historical linguistics.
Despite their popularity for phylogenetic reconstructions, gain-loss models have been used only sporadically in simulation studies. The only attempts that I know of so far are one study by Greenhill et al. (2009), where the authors used the TraitLab software (Nicholls 2013) to simulate language change along with horizontal transfer events, and a study by Murawaki (2015), in which (if I understand the study correctly) a gain-loss model is used to model language contact.
Another approach is reflected in the more "classical" work on lexicostatistics, where lexical change is modeled as a process of lexical replacement within previously selected concept slots. I will call this model the concept-slot model. In this model (and potential variants of it), a language is not a bag of words whose contents changes over time, but is more like a chest of drawers, in which each drawer represents a specific concept and the content of a drawer represents the words that can be used to express that given concept. In such a model, lexical change proceeds as a replacement process: a word within a given concept drawer is replaced by another word.
This model represents the classical way in which Morris Swadesh used to view the evolution of a given language. It is still present in the work of scholars working in the original framework of lexicostatistics (Starostin 2000), but it is used almost exclusively within distance-based frameworks, since a character-based account of the model would require a potentially large number of character states, which usually exceeds the number of character states allowed in the classical software packages for phylogenetic reconstruction.
Similar to the gain-loss model, there have not been many attempts to test the characteristics of this model in simulation studies. The only one known to me is a posthumously published letter from Sergei Starostin (1953-2005) to Murray Gell-Mann (Starostin 2007), in which he describes an attempt to account for his theory that a word's replacement rage increases with the word's age (Starostin 2000) in a computer simulation.
Problems with current models of lexical change
Neither the gain-loss model nor the concept-slot model seem to be misleading when it comes to describe the process of lexical change. However, they both obviously ignore specific and crucial aspects of lexical change that (according to the task stated above) any ambitious simulation of lexical change should try to account for. The gain-loss model, for example, deliberately ignores semantic change and morphological change. It can account for borrowings, which can be easily included in a simulation by allowing contemporary languages to exchange words with each other, but it cannot tell us (since it ignores the meaning of word forms) how the meaning of words changes over time, or how word forms change their shape due to morphological change.
The concept-slot model can, in theory, account for semantic change, but only as far as the concept-slots allow: the number of concepts in this model is fixed and one usually does not assume that it would change. Furthermore, while borrowing can be included in this model, the model does not handle morphological change processes.
In phylogenetic approaches, both models also have clear disadvantages. The main problem of the gain-loss model is the sampling procedure. Since one cannot sample all words of a language, scholars usually derive the cognate sets they use to reconstruct phylogenies from cognate-coded lexicostatistical word-lists. As I have tried to show earlier, in List (2016), this sampling procedure can lead to problems when homology is defined in a loose way. The problem of the concept-slot model is that it cannot be easily applied in phylogenetic inference based on likelihood models (like Maximum likelihood or Bayesian inference), since the only straightforward way to handle them would be multi-state models, which are generally difficult to handle.
Initial ideas for improvement
For the moment, I have no direct idea of how to model morphological change, and more research will be needed before we will be able to handle this in models of lexical change. The problem of the gain-loss and the concept-slot models to account for semantic change, however, can be overcome by turning to bipartite graph models of lexical change (see Newman 2010: 32f for details on bipartite graphs). In such a model, the lexicon of a human language is represented by a bipartite graph consisting of concepts as one type of node and word forms (or forms) as another type of node. The association strength of a given word node and a given concept node (or its "reference potential", see List 2014: 21f), ie. the likelihood of a word being used by a speaker to denote a given concept, can be modeled with help of weighted edges. This model naturally accounts for synonymy (if a meaning can be expressed by multiple words) and polysemy (if a word can express multiple meanings). Lexical change in such a model would consist of the re-arrangement of the weights in the network. Word loss and word gain would occur if a new word node is introduced into the network or an existing node gets dissociated from all of the concepts.
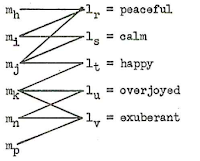 |
| Sankoff's (1996) bipartite model of the lexicon of human languages |
We can find this idea of bipartite modeling of a language's lexicon in the early linguistic work of Sankoff (1969: 28-53), as reflected in the figure above, taken from his dissertation (Figure 5, p. 36). Similarly, Smith (2004) used bipartite form-concept networks (which he describes as a matrix) in order to test the mechanisms by which these vocabularies are transmitted from the perspective of different theories on cultural evolution.
As I have never actively tried to review the large amount of literature devoted to simulation studies in historical linguistics, biology, and cultural evolution, it is quite possible that this blogpost lacks reference to important studies devoted to the problem. Despite this possibility, we can clearly say that we are lacking simulation studies in historical linguistics. I am furthermore convinced that the problem of handling lexical change in simulation studies is a difficult one, and that we may well have to wait to acquire more knowledge of the key processes involving lexical change in order to address it sufficiently in the future.
While I understand the popularity of gain-loss models in recent work on phylogenetic reconstruction in historical linguistics, I hope that it might be possible to develop more realistic models in the future. It is well possible that such studies will confirm the superiority of gain-loss models over alternative approaches. But instead of assuming this in an axiomatic way, as we seem to be doing it for the time being, I would rather see some proof for this in simulation studies, or in studies where the data fed to the gain-loss algorithms is sampled differently.
References
Bowern, Claire and Atkinson, Quentin D. (2012) Computational phylogenetics of the internal structure of Pama-Nguyan. Language 88: 817-845.
Cohen, Ofir and Rubinstein, Nimrod D. and Stern, Adi and Gophna, Uri and Pupko, Tal (2008) A likelihood framework to analyse phyletic patterns. Philosophical Transactions of the Royal Society B 363: 3903-3911.
Gévaudan, Paul (2007) Typologie des lexikalischen Wandels. Bedeutungswandel, Wortbildung und Entlehnung am Beispiel der romanischen Sprachen. Tübingen:Stauffenburg.
Gray, Russell D. and Jordan, Fiona M. (2000) Language trees support the express-train sequences of Austronesian expansion. Nature 405: 1052-1055.
Gray, Russell D. and Atkinson, Quentin D. (2003) Language-tree divergence times support the Anatolian theory of Indo-European origin. Nature 426: 435-439.
Gray, Russell D. and Greenhill, Simon J. and Ross, Malcolm D. (2007) The pleasures and perils of Darwinzing culture (with phylogenies). Biological Theory 2: 360-375.
Greenhill, S. J. and Currie, T. E. and Gray, R. D. (2009) Does horizontal transmission invalidate cultural phylogenies? Proceedings of the Royal Society of London, Series B 276: 2299-2306.
Lees, Robert B. (1953) The basis of glottochronology. Language 29: 113-127.
List, Johann-Mattis (2016) Beyond cognacy: Historical relations between words and their implication for phylogenetic reconstruction. Journal of Language Evolution 1: 119-136.
Murawaki, Yugo (2015) Spatial structure of evolutionary models of dialects in Contact. PLoS One 10: e0134335.
Newman, M. E. J. (2010) Networks: An Introduction. Oxford: Oxford University Press.
Nicholls, Geoff K and Ryder, Robin J and Welch, David (2013) TraitLab: A MatLab package for fitting and simulating binary tree-like data.
Ronquist, Frederik and Huelsenbeck, J. P. (2003) MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics 19: 1572–1574.
Sagart, Laurent, Jacques, Guillaume, Lai, Yunfan, Ryder,
Robin, Thouzeau, Valentin, Greenhill, Simon J., List,
Johann-Mattis (2019) Dated language phylogenies shed light on the
ancestry of Sino-Tibetan. Proceedings of the National Academy of Science of the United States of America 116: 10317–10322. DOI: 10.1073/pnas.1817972116
Sankoff, David (1969) Historical Linguistics as Stochastic Process. McGill University: Montreal.
Smith, Kenny (2004) The evolution of vocabulary. Journal of Theoretical Biology 228: 127-142.
Starostin, Sergej Anatolévič (2000) Comparative-historical linguistics and lexicostatistics. In: Renfrew, Colin, McMahon, April, Trask, Larry (eds.): Time Depth in Historical Linguistics: 1. Cambridge:McDonald Institute for Archaeological Research, pp. 223-265.
Starostin, Sergej A. (2007) Computer-based simulation of the glottochronological process (Letter to M. Gell-Mann). In: : S. A. Starostin: Trudy po yazykoznaniyu [S. A. Starostin: Works in Linguistics]. LRC Publishing House, pp. 854-861.
Swadesh, Morris (1952) Lexico-statistic dating of prehistoric ethnic contacts. With special reference to North American Indians and Eskimos. Proceedings of the American Philosophical Society 96: 452-463.
Swadesh, Morris (1955) Towards greater accuracy in lexicostatistic dating. International Journal of American Linguistics 21.2: 121-137.

No comments:
Post a Comment