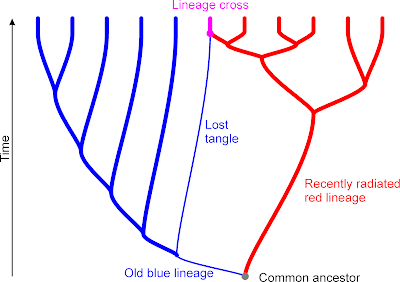
A critical question in phylogenetics, and this applies to both the detection and inference of reticulation, is: How much trust do we put in the inferred tree? A phylogenetic tree is just the simplest of all possible phylogenetic networks. Let's assume that there was some phylogenetic reticulation in the past (lineage mixing and crossing), then, in the best-case scenario, our inferred tree shows one of the intertwining pathways but misses the tangles, the crossroads.
In the worst case, summarizing data with substantially different signals will give us branching artifacts such as:
- terminal branches that are too long,
- too long internal branches with conspicuously low support (ie. BS << 100, PP < 1.0),
- artificial branches representing the least-conflicting solution for the conflicting data,
- low branch support in general.
Topological incongruence between gene trees and parental genealogies (as above) is commonly taken as evidence for reticulation. If one gene provides high support for taxon A as sister to B, and another gene has high support for B as sister to C, then B is likely the product of reticulation (eg. hybridization)
One simple possibility to put together a phylogenetic network is to summarize all of the trees in the form of a Consensus network, as shown next. (Technically this is a splits graph, it becomes a phylogenetic network as soon as we determine a root, which, here, would be at the edge leading to the Giant Panda.)
 |
| A strict Consensus network of the paternal, biparental, and maternal bear genealogies. The numbers show the non-parametric bootstrap support for each (competing) split. |
In this case, low support for a branch in a combined tree (the values on top) can result from strong conflict. For instance, the brownish splits, which are poorly supported using the combined data (BS = 21, 29), receive near unambiguous support from the mitochondrial genes, but are largely or entirely rejected by the Y-chromosome and nc-intron data. In the combined tree, this deep conflict is resolved by introducing the artificial red clade, with similarly low support: the signal in the data is ambiguous and they support splits between equally possible alternatives.
We know lineage crossing took place in bears (the mitochondrial and Y-chromosome tree are very much in conflict). However, does the above mean that earliest bear-ish creatures hybridized, too? Note that the conflict is associated with a short-branched part of the graph, where apparently little evolution happened. Fast ancient radiations usually come with incomplete lineage sorting and diffuse signals. The only data set producing longer roots, but with notably lower support, are the biparentally inherited introns.
We are closing in our own tail and have to ask again: Is this low support in the autosomal intron tree due to internal conflict, (sets of) introns preferring different topologies, supporting an ancient mixing hypothesis, or just reflecting lack of resolution? Check out the original paper by Kutschera et al. (2014, Mol. Biol. Evol. 31: 2004–2017), and make up your own mind.
On to the angiosperms
In my last post, I exemplified what Walker et al. (PeerJ, 2019) found in their angiosperm study: when we look at a plastome tree we are not looking at a summary of all gene trees but instead at a topology forced by very few of the genes in the chloroplast genome, such as the matK. We also have seen that one misplaced sequence (outgroup Podocarpus-matK) doesn't affect at all the combined analysis — it didn't even reduce the ingroup - outgroup split support. Also, I noted that the low-supported part of the combined tree goes hand in hand with lack of decisive signal from the matK.
It's time to take a look at what the other genes in this example data set come up with.
One thing is obvious: for most genes (except the nuclear-encoded rRNA genes) including the outgroup taxa adds little ingroup information of use — they are just too distant to any of the ingroup taxa. Outgroup rooting is tricky for angiosperms. Outgroup taxa will always be attracted to the ingroup taxon that is the least similar to any other part of the ingroup: Amborella in this case.
Generally, all of the ANA-grade water plants are genetically distinct and topologically isolated; any outgroup-inferred root must be placed in this part of the tree (all other living seed plants are very distant relatives of angiosperms looking back at, at least, ~250 million years of independent evolution, see eg. Age of Angiosperms... and What is an angiosperm pt. 2). The relatively conserved plastid rbcL and mitochondrial matR prefer an Amborella-Nympheales clade as sister to all other angiosperms, while the more divergent atpB, plastid, nad5, mitochondrial, and 25S, nuclear, prefer the Amborella-root — this is a direct indication for ingroup-outgroup long-branch attraction. Any other placement of the outgroup subtree within the ingroup would necessarily decrease the likelihood of the tree (but note the position of the root in the 18S tree, lower-left the tree based on the most-conserved, evolution-constrained gene in our sample; see also All solved a decade ago..., fig. 4A).
We can look at these trees with the strict consensus network, using uninformed edge lengths— that is, the network counterpart to the strict consensus cladograms still common in plant phylogenetic literature.
This is a nice piece of computer-art, but is scientifically quite useless (the boxiness and general graph structure is, however, reminiscent of strict consensus networks of most-parsimonious tree samples inferred for extinct animals, one example, and plants).
We can add some discriminatory information by counting how often each split occurs in the set of gene trees.
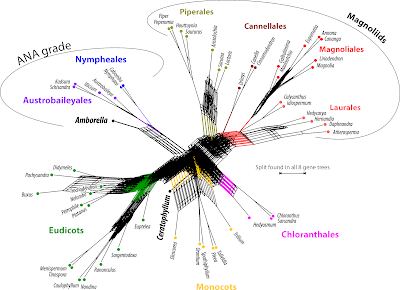 |
| Same set of tree, different way of summarizing it. Note how the main clades emerge: one or two genes may have misplaced the one or other OTU but the others get it right. |
Alternatively, we can average the actual tree branch lengths to inform the edge length of the consensus network.
A pretty little thicket of trees. Some agreement is found towards the leaves, but even here we have conflict among the gene trees. In some trees, there are long branches grouping non-related OTUs, obvious tree inference artifacts. The general rule is that the deeper we go (ie. the farther back in time), the messier it gets. Adding to this is that, irrespective of which gene is used, some OTUs are much closer to the hypothetical common ancestor (of Mesangiosperms, ie. all but ANA grade) than others – in the eudicots, the least-evolved taxa are Platanus (very old tree genus) and Euptelea (the basalmost Ranunculales); in the Magnoliales, the only angiosperm clade that lacks synapomorphies, it's Magnolia and Liriodendron (again, very old and primitive tree genera). Darwin's Abominable Mystery, the sudden appearance and quick dominance of angiosperms, resulted in an abominable chaos of gene trees and signals. How can they possibly converge to a single tree with amply high support along most branches?
 |
| The combined tree from the first post. |
I argue here that, if there had been substantial reticulation messing up the signal of contemporary lineages and reflecting decoupled histories (like in the case of bears), we would expect at least some (artificial) branching patterns with low support in the combined tree, as well. This would also be the case looking at the gene-tree consensus networks, not only in the deepest parts but also closer to the leaves.
We will be explore this alternative hypothesis in the next (and final) post of this mini-series.





No comments:
Post a Comment