Using median networks to understand evolution of genera

Median networks and their derivatives, such as median-joining and reduced median networks, are frequently used when studying genetic patterns within species. Indeed, this is what they were originally designed for. But occasionally, researchers have used them one taxonomic level up, to illustrate inter-specific relationships. For this blog post, I have dug out some reconstructions I made that I found quite interesting in this regard (including one that made it into publication), which I will discuss as examples.

Genetic markers

When working at the tips of the Tree of Life, where it becomes quite bushy, the messiness of species and permeability of species boundaries is one important issue. But another one is that we lack suitable genetic markers to collect data — we need gene regions that are variable enough to elucidate both intra- and inter-species differentiation patterns using tree inference.

One all-time classic marker is the nuclear-encoded ITS region, but this can be a multi-edged sword. Nuclear genomes usually include thousands of tandemly arranged repeats of the 35S rDNA, which includes the ITS region, in what is called the Nucleolus Organizer Region (NOR). The repeats may or may not be homogenized via concerted evolution. Furthermore, quite a few plants have more than one NOR, so we are dealing with paraloguous ITS sequences – in the strict genetic sense, these are sequences amplified from different loci (and chromosomes). In polyploids, we have ITS homoeologues passed on from the original donors. For instance, grasses can have four homoeologue NORs and ITS sets (usually adressed as "paralogues" in phylogenetic literature).

Even when not struggling with multiple ITS variants (intra-genomic variation), we can see the backside of concerted evolution: low ITS divergence in not a few plant genera. When ITS doesn't provide enough signal, researchers sometimes sequence the 3' end of the supposedly more variable 5'-external transcribed spacer of the 35S rDNA, the 5'-ETS (or just "ETS"). As an important terminological note: it is the 5'-ETS because there is another ETS at the end of the 35 S rDNA cistron, the 3'-ETS (essentially unknown except for organisms where the entire nuclear rDNA tandem repeat has been sequenced). Sequences uploaded to gene banks usually show the (repeat-free, or repeat-poor) 3' half and not the entire 5'-ETS, which has confused more than one researcher / reviewer — most but not all 3'-ETS sequences stored in gene banks are 5'-ETS.

When it comes to plastids, the currently best-covered most-variable marker is the trnH-psbA intergenic spacer, which includes prominent length polymorphic sections, which can be tricky to align once we go above the genus level (sometimes even within genera). The old plastic classic, the trnL/LF region, including the trnL intron and downstream trnL-trnF spacer, is probably the most sequenced plastid gene region; but it is usually too conservative to resolve even distantly related species of the same genus. Recently, many other alternatives have been recruited, thanks to completely sequenced plastomes.

Traditional intra-generic studies infer trees that often lack support at crucial branches, for two reasons:

1. The authors overlooked (or ignored) incongruent signal from the combined gene regions (you wouldn't believe how many ITS-trnL/LF-backed published trees are fundamentally flawed);
2. Many branches are supported by a single or very few mutational patterns (which is one reason why you see still a lot of cladograms in such studies, rather than phylograms showing the branch lengths).

Reason 2 does have a benefit, however — you may have unambiguous support for a branch collecting individuals (species) that are virtually identical.

Why median-networks?

When we are very close to the leaves of the Tree of Life, we work with faint primary signals, and often face very flat likelihood surfaces of the (inferred) tree space. When the rate of change is low, parsimony can out-compete probabilistic methods, in the sense that the inferred trees (or networks, as we will see below) are more informative. Median-networks apply the parsimony principle to reticulating relationships. However, in contrast to parsimony-optimized trees, (full) median-networks:

• include all equally parsimonious solutions to explain the data;
• can place taxa at internal nodes (the medians) — they can treat a sequence as ancestral to another.

Nevertheless, all species are contemporaneous, so they can't be each other's ancestors, right? Theoretically yes, but in reality, they actually can. When inferring species trees, we ignore the idea that one species may actually represent the remainder of an ancestral (paraphyletic) species after one (or more) populations became isolated. So, one living species can appear to be ancestral to another.

Another important point is that each (intra)specific lineage may have evolved at a different pace. We may thus find sequences in modern species that are much more primitive than are those of others (genetic "symplesiomorphies", if you want). The most striking example of a genetic symplesiomorphy that crossed my path was a 200-nt 18S fragment sequenced from a seedling found in a sea-locked cave. The people who sequenced it found best-BLAST hits with "basal" angiosperms, which didn't fit their matK fragment. This result was confirmed by re-sequencing, so they asked me to look at the data. I readily saw that the 18S fragment is from a core region, virtually identical across quite a range of angiosperms, including the group with a matching matK sequence. The ITS then showed that the matK's identification of the order (Myrtales) was correct, and that it was a Syszygium.

Fig. 1. A (reduced) phylogeny of Hoya (wax plants); one of the many intra-generic trees I inferred. Several unchallenged clades emerged (collapsed) as well as low-supported branches (grey backgrounds). A bootstrap consensus network revealed that the low support relates to semi-(in)congruent signals from the underlying matrix (including ITS, 5'-ETS, trnT-trnL, and trnL/LF data; see this post why you don't find this and the following graphs in the finally published paper: Wanntorp et al. 2014)

Example 1: Hoya

In the above tree (Fig. 1) the low support partly relates to incongruent nuclear and plastid signals from 'rogue' OTUs — these may be species / individuals, but it's typically just one individual per species. However, in other cases the signal from either the nuclear or the plastid data is simply ambiguous (not contrasting with the other part of the data) or semi-(in)congruent — the general affinity is the same but when it comes to exact placement, the nuclear data supports a different topology than the plastid data (Fig. 2).

Fig. 2. Maximum-likelihood bootstrap consensus networks for the complete plastid (A; trnT-trnL; trnL/LF) and nuclear (B; ITS + 5'ETS) data sets. Clades labelled only in one graph have little support (BS < 20) based on the other data. For example, there is no plastid counterpart to nuclear clades N and O, the taxa are scattered within the (cp-)H clade (but compare with Fig. 1! Pure data combination magic: strong support + ambiguity = equal or stronger support).

The failure to resolve e.g. the proximal relationships within the red clade and its relationship with respect to the blue clade and several minor clades (isolated OTUs) coloured pink in Fig. 2 (or resolution issues within the yellow-greenish bunch) has indeed to do with ambiguous signals due to less- and more-derived sequences.

Fig. 3. (Filtered) median-joining networks for each gene region. The graphs depict which clade has distinct (unique) sequence patterns, and can be interpreted regarding the potential evolution of the analysed gene regions. High(er) divergent markers: A, ITS1; B, trnT-trnL; low divergent markers: C, ITS2; D, trnL intron; E, trnL-trnF spacer.

At the genus level, these data are quite divergent (hence the tree in Fig. 1), and applying a median-joining network (or even reduced median) is computationally not feasible. So, in order to put their sequence variants into perspective, I filtered all group-specific site variations from the gene regions (singleton and unique mutations found only in a few members of a clade, or shared by a single OTU per clade, clade-unspecific stochastic convergences, are not considered). The complete data (raw and tabulated) can be found at figshare (Grimm 2017).

We can make some interesting observations. The pink species, OTUs attracted equally to the red and blue clades, have essentially underived or less derived sequence variants, either shared with or ancestral to the sequences of the red and blue clades. This applies to a more general degree also to the white species, highly ambiguous OTUs with no clear affinity to one of the major clades. The lack of unique shared genetic traits with any differentiated clade is the reason they are placed within the poorly supported, root-proximal ("basal") part of the tree(s).

Fig. 4. A tanglegram of the all-OTU plastid (left) and nuclear trees. Colouring as above (black font equals white in Fig. 3)

Another thing is that we can see that neither the main sequence features of clade III or IV, compared to clade V and VI, are consistently more primitive than their sister. They are proper sister clades that evolved from a common origin, but not from each other (via "budding"). This is something not obvious from the inferred trees (see Fig. 4). The pink sequences, scattered across the root-proximal ("basal") parts of the clade including pink, red, and blue OTUs are closer to the common ancestor shared with V (blue) and VI (red), but are obviously isolates from a first radiation round (note their position in Fig. 3A, D vs. B, C, and E and Fig. 4).

Example 2: Indomalayan and Australasian Ixora

This is a classic example of using median networks.

Ixora is a genus of Rubiaceae with a wide distribution in the tropics and subtropics of the Old World. As in the case of Hoya, I was recruited for the Banag et al. (2017) paper because the genetic differentiation patterns were very promising, but eluded the limited capacities of traditional tree inference.

The focus of the study was to find out how the high diversity of the genus in the Phillipine archipelago fits into the general framework of the genus. In contrast to Hoya (example 1) there is a (single) deep, well-supported incongruence between the nuclear (ITS, 5'-ETS) data set and the plastid data set (rps16 intron and the entire trnT–F region, as in the case of Hoya).

Fig. 5. Nuclear-plastid tanglegram for our Ixora dataset (Banag et al. 2017, fig. 1) Nuclear clade III is not found in the 'best-known' ML tree, but of the bootstrap (BS) sample preferred alternative (never ignore the BS consensus networks [nuclear/plastid], when facing low-supported branches in trees!)

In Ixora, we dealt with a number of main clades showing different nuclear-plastid combinations: I/A – red; I/B1 – orange; II/B2 and II/B3 – green; III/C – blue; IV/B (cultivars, not included in Fig. 5, showed additional combinations). Geographically, this leads to a compelling pattern (Fig. 6).

Fig. 6. Geographic maps of the genotyped samples (Banag et al. 2017, fig. 4). A. Nuclear data, B. Plastid data.

But to really trace the geographic-evolutionary sources of the highly diverse Philippine species set, which included members of nearly all lineages (except for the Afro-indian III/C), we had to deal with coherent but very few mutational patterns in the plastid gene regions. In contrast to the spacers of the 35S rDNA, plastid signatures are inherited maternally. Seeds often (but not always) travel less distance than pollen, and hence plastid differentiation in plants reflects primarily provenance. With respect to the low divergence, (nearly unfiltered) median-joining networks were a natural choice. Fig. 7 shows the close-up on the Philippines with the relevant plastid-based networks.

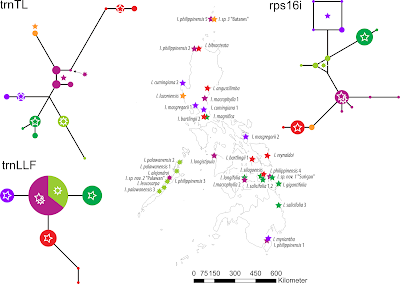Fig. 7. Plastid-based median-joining (haplotype) networks for Ixora and their geographic distribution across the Philippine archipelago (Banag et al. 2017, fig. 5).

One observation here is that the trnTL reflects the isolation of the green species on Palawan (the island to the left), which tectonically is not a part of the Philippines. On the other hand, the trnLLF and rps16i of the green (dark green) species in Philippine proper derive from that of their Palawan counterparts, reflecting a stepwise colonization by the green lineage.

We also note that the red haplotypes representing lineage I/A unique to the Philippines are derived in comparison to the main purple type found all across the larger region, hinting towards a relatively long isolation time. This explains the topology of the plastid-based tree (Fig. 5) and its resolution issues. The purple haplotypes don't form distinct clades, because they are sequentially intermediate between the distinct sister clades (I/A, I/B1) and the equally widespread green lineage (IV/B2,B3).

Example 3: Western Eurasian species of Quercus subgenus Cerris section Ilex ('Ilex oaks')

This is a much more "beyond the edge" example of using median networks.

Differentiation patterns in the multicopy tandem-repeated nuclear spacers can be extremely challenging. In Göker & Grimm (2008) and Potts et al. (2014) we proposed network-based and network-affine methodological frameworks for how to deal with it. However, I did also explore the potential of median networks and their derivatives when applied close to the species level.

One particularly puzzling case is the species aggregate of Quercus aucheri, Q. coccifera, and Q. ilex, a group of wide-spread Mediterranean oaks (see also Simeone et al. 2016, and Vitelli et al. 2017 including median-joining networks). Q. ilex-type oaks have been co-dominant elements of the Mediterranean flora long before the Mediterranean became summer-dry (Denk et al. 2017).

For a never-published detailed study of Moroccan Q. ilex, I generated (essentially unreduced) median networks (following the protocol of Bandelt, Macaulay & Richards 2000) for two data sets of cloned ITS and 5S-IGS sequences, capturing intra- and inter-individual variation in the species and its sister species. 5S-IGS refers to the non-transcribed intergenic spacer of the 5S rDNA tandem repeats, a gene cluster delocalized from the NOR in most modern seed plants (in Ginkgo, for example, it's still located in the non-transcribed spacer between two 35S rDNA cistrons). As far as studied, oaks can have one or more loci per haplome encoding for the 5S rDNA repeats (and NORs; Ribeiro et al. 2011).

The main reason for this work was that I wanted to define ITS and 5S-IGS genotypes ("ribotypes") and to see how they map proportionally. The median networks appear quite complex at first sight (and possibly second and third, as well, when you are not the one who made them). Fig. 8 shows the median network for the 5' ITS1, which is the part of the ITS that sticks with the 18S pre-rRNA during the rDNA maturation process.

Fig. 8. A non-reduced median network for the 5' half of the ITS1 of western Eurasian Quercus ilex. Genotypes occurring in more than a single clone are coloured and numbered (1–15), coloured 4-digit numbers refer to individual clones (singletons), numbers at edges refer to the nucleotide site in the alignment showing the mutational pattern (convergent mutations in red font).

The mutational pathways don't seem to be overly complex, and the same holds for the other two non-coding, transcribed parts (functionally speaking) of the ITS region (3'-ITS1 and ITS2) and the 5S-IGS (Fig. 9).

Fig. 9. A non-reduced median network for the 5S-IGS data. Abbreviations refer to geographic regions, everything else as in Fig. 8 (the colours indicate no relation across the two figures)

Using such reconstructions as a basis, it is possible to make pie charts reflecting the frequency of the so-defined main genotypes (those with identical colours in Figs 8 and 9), and put them into a simple correlation graph (Figs 10, 11).

Fig. 10. Pie charts summing up the frequency of ITS genotypes (cf. Fig. 8) per geographic region/place.

Fig. 11. Correlation between 5S-IGS (Fig. 9) and ITS genotypes. Types with no links refer to individuals only covered for one of the data sets (thanks to the go-abroad policy of the German Science Foundation when becoming too good, I could not apply for a new project and had to leave the country, hence, lost my technician and lab and any possibility to fill the gaps)

Take-home message (actually: a call)

If you have data suitable to make median networks such as

• overall low divergence
• slow rate of change

or other beneficial situations for doing parsimony analyses, just give it a try. The more papers that are published showing such results, the easier it will become to get them past the confidential peer review. They can be a most versatile tool to understand molecular evolution, and the prospects and perils in our inferred trees, or competing support patterns (if you're already beyond tree-thinking).


There are further avenues that could be explored using the median network family. I already pointed out in an earlier post that they can depict the true tree when it comes to morphological data of modern-day taxa and their potential ancestors.

Another interesting thing would be to apply them to above-genus data sets when dealing with (very) slow evolving gene regions such as the 5.8S rDNA. For instance, backed by networks (median or others), one can see that the highly similar 18S rDNA of Juglandaceae and Myricaceae is likely a genetic plesiomorphy (which is one reason for the ambiguous support in oligo-gene Fagales trees).

Links

Download page for NETWORK, the free-software package I used to generate all of the median networks — http://www.fluxus-technology.com/sharenet.htm

What I was not allowed to show in #2: Networks explaining molecular evolution in wax plants — https://researchinpeace.blogspot.fr/2017/12/what-i-was-not-allowed-to-show-2.html

(If you have more links, feel free to comment/contact: Let's make median networks great again #MeNeGA)

References

Banag CI, Mouly A, Alejandro GJD, Bremer B, Meve U, Grimm GW, Liede-Schumann S (2017) Ixora (Rubiaceae) on the Philippines – crossroad or cradle? BMC Evolutionary Biology 17:131.

Bandelt H-J, Macaulay V, Richards M (2000) Median Networks: speedy construction and greedy reduction, one simulation, and two case studies from human mtDNA. Molecular Phylogenetics and Evolution 16:8-28.

Denk T, Velitzelos D, Güner HT, Bouchal JM, Grímsson F, Grimm GW (2017) Taxonomy and palaeoecology of two widespread western Eurasian Neogene sclerophyllous oak species: Quercus drymeja Unger and Q. mediterranea Unger. Review of Palaeobotany and Palynology 241:98-128.

Göker M, Grimm GW (2008) General functions to transform associate data to host data, and their use in phylogenetic inference from sequences with intra-individual variability. BMC Evolutionary Biology 8:86.

Grimm G. 2017. Over-the-edge tables and reconstructions linked to the slimmed-down paper of Wanntorp et al. (2014), published in Taxon. figshare. https://doi.org/10.6084/m9.figshare.5688181.v1

Potts AJ, Hedderson TA, Grimm GW (2014) Constructing phylogenies in the presence of intra-individual site polymorphisms (2ISPs) with a focus on the nuclear ribosomal cistron. Systematic Biology 63:1-16.

Ribeiro T, Loureiro J, Santos C, Morais-Cecílio L. 2011. Evolution of rDNA FISH patterns in the Fagaceae. Tree Genetics and Genomes 7:1113–1122.

Simeone MC, Grimm GW, Papini A, Vessella F, Cardoni S, Tordoni E, Piredda R, Franc A, Denk T (2016) Plastome data reveal multiple geographic origins of Quercus Group Ilex. PeerJ 4:e1897.

Vitelli M, Vessella F, Cardoni S, Pollegioni P, Denk T, Grimm GW, Simeone MC (2017) Phylogeographic structuring of plastome diversity in Mediterranean oaks (Quercus Group Ilex, Fagaceae). Tree Genetics and Genomes 13:3.

Wanntorp L, Grudinski M, Forster PI, Muellner-Riehl AN, Grimm GW (2014) Wax plants (Hoya, Apocynaceae) evolution: epiphytism drives successful radiation. Taxon 63:89-102.