Admixture graphs – evolutionary networks for population biology

Current methods for evolutionary networks include: (i) combining trees, clusters or triplets into what is usually called a hybridization network (but could also be a horizontal gene transfer network, HGT), and (ii) decomposing ordered character data into what is called a recombination network (or ancestral recombination graph). Much work on these two approaches has been carried out recently within the bioinformatics community, and this is continuing.

However, the biology community has sometimes taken a different approach. Notably, work has concentrated on constructing models for detecting reticulation events in various types of molecular data, such as comparative genome analysis for HGT, or quantifying inter-population gene flow (eg. due to migration). A network is then manually constructed by adding reticulation branches to a phylogenetic tree of the organisms concerned. Indeed, in many cases the network diagram is not presented explicitly in the publications, but is merely implied from a list of the sources and sinks of the gene flows detected.

The network model for this latter type is thus essentially "a tree obscured by vines", although the network can actually become rather complicated. The basic idea has a long history (Lathrop 1982), although it has only recently become popular. In this blog post I highlight one line of recent work that takes this approach, which involves admixture graphs in population genetics.

Introduction

Historically, population genetics has concentrated on estimating various population parameters from quantitative models of gene history, notably rates of population expansion/contraction, rates of migration, timing of divergence, and presence/absence of bottlenecks. This is rarely done in any graphical way, relying instead on summary statistics. Alternatively, graphical methods such as principal components analysis and agglomerative clustering have been used to summarize the genetic data, and from this summary various scenarios can be deduced post hoc about possible population history (e.g. Skoglund and Jakobsson 2011; Hodoglugil and Mahley 2012).

However, more recently, explicit models of historical gene flow between populations have been developed, usually within the context of generalizing a phylogenetic tree. A tree can be used to represent historical relationships in the absence of significant amounts of gene flow, but not otherwise. So, the general approach has been to use a tree as the null model (representing absence of gene flow), and then testing how many reticulation events are needed to significantly improve the fit of the data to an increasingly complex network. The resulting diagram is called an admixture graph, which thus models both population divergence and gene flow. The reticulations represent the different proportions of genetic mixing between pairs of populations.

A model of population separation and admixture, from Reich et al. (2011) p. 522.

Methods

There are several computer programs that quantify population structure in the presence of admixture between populations, such as the models used in the older programs Structure, BAP5 and TESS (see François and Durand 2010), as well as in more recent programs like Admixture (Alexander et al. 2009). However, the most recent programs have been developed specifically to deal with network analysis of genome-wide single nucleotide polymorphism (SNP) data. The populations studied will usually be within a single species, but this need not be so.

The TreeMix program (Pickrell and Pritchard 2012) is described by the authors as follows: "Our goal is to provide a statistical framework for inferring population networks that is motivated by an explicit population genetic model, but sufficiently abstract to be computationally feasible for genome-wide data from many populations (say, 10-100) ... Our approach to this problem is to first build a maximum likelihood tree of populations. We then identify populations that are poor fits to the tree model, and model migration events involving these populations." This process proceeds as for the standard tree-based approach except that the likelihood model also includes migration weights: "Estimation involves two major steps. First, for a given graph topology, we need to find the maximum likelihood branch lengths and migration weights. Second, we need to search the space of possible graphs. [For] a given graph topology, we iterate between optimizing the branch lengths and weights ... [Then,] to search the space of possible graphs, we take a hill-climbing approach."

This method has been used by, for example, Pickrell et al. (2012).

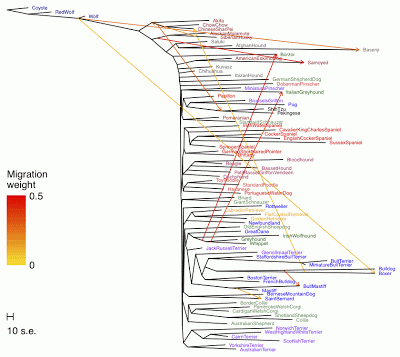Inferred dog breed admixture graph, from Pickrell and Pritchard (2012).

The AdmixTools program (Patterson et al. 2012), as claimed by the authors, "has some similarities to the TreeMix method but differs in that TreeMix allows users to automatically explore the space of possible models and find the one that best fits the data (while our method does not), while our method provides a rigorous test for whether a proposed model fits the data (while TreeMix does not)." The explicit testing of the fit of data and model is "based on studying patterns of allele frequency correlations across populations. The 3-population test is a formal test of admixture and can provide clear evidence of admixture, even if the gene flow events occurred hundreds of generations ago. The 4-population test ... is also a formal test for admixture, which can not only provide evidence for admixture but also provide some information about the directionality of the gene flow. The F4 ratio estimation allows inference of the mixing proportions of an admixture event".

This approach has been used by Reich et al. (2009, 2011, 2012).

Distinct streams of gene flow from Asia into America, from Reich et al. (2012) p. 372.

These methods have not yet been subjected to any critical evaluation independently of their developers, although various blog authors have been actively investigating them (e.g. these posts by Dienekes Pontikos: 1, 2, 3). The general approach, of adding reticulations to an initial tree, is reminiscent of that taken by the T-Rex program to produce reticulograms, which has been subject to criticisms (Gauthier and Lapointe 2002, 2007; Huson et al. 2011), some of which may apply to the admixture methods as well.

References

Alexander D.H., Novembre J., Lange K. (2009) Fast model-based estimation of ancestry in unrelated individuals. Genome Research 19: 1655-1664.

François O., Durand E. (2010) Spatially explicit Bayesian clustering models in population genetics. Molecular Ecology Resources 10: 773-784.

Gauthier O., Lapointe F.-J. (2002) A comparison of alternative methods for detecting reticulation
events in phylogenetic analysis. In: Jajuga K., Sokolowski A., Bock H.-H. (eds) Classification, Clustering, and Data Analysis: Recent Advances and Applications, pp. 341-347. Springer, Berlin.

Gauthier O., Lapointe F.-J. (2007) Hybrids and phylogenetics revisited: a statistical test of hybridization using quartets. Systematic Botany 32: 8-15.

Hodoglugil U., Mahley R.W. (2012) Turkish population structure and genetic ancestry reveal relatedness among Eurasian populations. Annals of Human Genetics 76: 128-141.

Huson D.H., Rupp R., Scornavacca C. (2011) Phylogenetic Networks: Concepts, Algorithms and Applications. Cambridge University Press, Cambridge.

Lathrop G.M. (1982) Evolutionary trees and admixture: phylogenetic inference when some populations are hybridized. Annals of Human Genetics 46: 245-55.

Patterson N.J., Moorjani P., Luo Y., Mallick S., Rohland N., Zhan Y., Genschoreck T., Webster T., Reich D. (2012) Ancient admixture in human history. Genetics (in press).

Pickrell J.K., Patterson N., Barbieri C., Berthold F., Gerlach L., Lipson M., Loh P.-R., Güldemann T., Kure B., Mpoloka S.W., Nakagawa H., Naumann C., Mountain J.L., Bustamante C.D., Berger B., Henn B.M., Stoneking M., Reich D., Pakendorf B. (2012) The genetic prehistory of southern Africa. Unpublished ms.

Pickrell J.K., Pritchard J.K. (2012) Inference of population splits and mixtures from genome-wide allele frequency data. Unpublished ms.

Reich D., Patterson N., Campbell D., Tandon A., Mazieres S., Ray N., Parra M.V., Rojas W., Duque C., Mesa N., García L.F., Triana O., Blair S., Maestre A., Dib J.C., Bravi C.M., Bailliet G., Corach D., Hünemeier T., Bortolini M.C., Salzano F.M., Petzl-Erler M.L., Acuña-Alonzo V., Aguilar-Salinas C., Canizales-Quinteros S., Tusié-Luna T., Riba L., Rodríguez-Cruz M., Lopez-Alarcón M., Coral-Vazquez R., Canto-Cetina T., Silva-Zolezzi I., Fernandez-Lopez J.C., Contreras A.V., Jimenez-Sanchez G., Gómez-Vázquez M.J., Molina J., Carracedo A., Salas A., Gallo C., Poletti G., Witonsky D.B., Alkorta-Aranburu G., Sukernik R.I., Osipova L., Fedorova S.A., Vasquez R., Villena M., Moreau C., Barrantes R., Pauls D., Excoffier L., Bedoya G., Rothhammer F., Dugoujon J.M., Larrouy G., Klitz W., Labuda D., Kidd J., Kidd K., Di Rienzo A., Freimer N.B., Price A.L., Ruiz-Linares A. (2012) Reconstructing Native American population history. Nature 488: 370-374.

Reich D., Patterson N., Kircher M., Delfin F., Nandineni M.R., Pugach I., Ko A.M., Ko Y.-C., Jinam T.A., Phipps M.E., Saitou N., Wollstein A., Kayser M., Pääbo S., Stoneking M. (2011) Denisova admixture and the first modern human dispersals into Southeast Asia and Oceania. American Journal of Human Genetics 89: 516-528.

Reich D., Thangaraj K., Patterson N., Price A.L., Singh L. (2009) Reconstructing Indian population history. Nature 461: 489-494.

Skoglund P., Jakobsson M. (2011) Archaic human ancestry in East Asia. Proceedings of the National Academy of Sciences of the USA 108: 18301-18306.