Phylogenetic networks: Best student thesis

At the recent conference of the Landelijk Netwerk Mathematische Besliskunde (Dutch Network on the Mathematics of Operations Research) it was announced that Leo van Iersel (now at Centrum Wiskunde & Informatica, in Amsterdam) was awarded the Gijs de Leve Prize for best operations research Ph.D. thesis of the last 3 years.

 Leo’s thesis, submitted in January 2009 to the Technische Universiteit Eindhoven, covers single individual haplotyping, population haplotyping, and phylogenetic networks. As part of the award Leo gave a talk on "Phylogenetic Networks: Reconstructing Evolution" [PDF of the slides].

Apparently, phylogenetic networks are now being treated as a respectable part of mathematics. This is a not inconsiderable step. Phylogenetics has not hitherto been a notable component of discrete mathematics, although discrete mathematics, particularly combinatorics, has long been a major part of phylogenetics.

Reviews of recent books

The first book to make an appearance that explicitly deals with phylogenetic networks was:

D. H. Huson, R. Rupp and C. Scornavacca (2011) Phylogenetic Networks: Concepts, Algorithms and Applications. Cambridge University Press. [Dated 2010 but published January 17 2011] Available in hardback ISBN:978-0-521-75596-2 and as an eBook ISBN:978-0-511-92242-8.

In addition to the three reviews that appear as part of the publisher's blurb, a number of independent book reviews have appeared since its publication:

Tiratha Raj Singh (2011) Current Science 100: 1570-1571.

Paul Cull (2011) Computing Reviews Review#139416.

Steven Kelk (2012) Systematic Biology 61: 174-175.

Jim Whitfield (2012) Systematic Biology 61: 176-177.

These are all worth reading, but I wish to comment here on one particular review, the one by Steven Kelk. This review makes two points about current network methods that seem to me not to have been sufficiently emphasized in other publications. The review itself is thus an important contribution to the literature on phylogenetic networks.

(1) Rooted networks based on a "hybridization" model can be derived by combining clusters, triplets or trees. [Note: combining characters usually leads to a "recombination" model.] However, only by combining trees do the reticulation vertices in the resulting network explicitly model reticulate evolutionary events (e.g. hybridization or horizontal gene transfer); for clusters and triplets the reticulation vertices can be abstract. This has important practical consequences for biologists, who routinely interpret rooted networks as though all of the vertices (nodes) represent inferred ancestors undergoing "descent with modification" (as Charles Darwin called it). There has been insufficient attention paid to this point in the literature on cluster and triplet methods.

Note that this point does not deny any intrinsic mathematical interest in clusters and triplets (which Steven, himself, emphasizes in his own research work). Nor does it deny any possible use of them in practical network methods; indeed, I have seen them work quite well in practice. The point is simply that the tree model explicitly provides something that biologists find valuable, and which (I would argue) has been principally responsible for the widespread use of that model in phylogenetics. One can even argue that phylogenetic analysis is the inference of vertices in a tree/network. (If you look at Darwin’s only published tree you will note that it is the vertices of his tree that are missing, indicating his explicit doubt about the feasibility of inferring them.)

(2) Great attention has been paid in the literature to certain topologically restricted sub-families of rooted networks (such as galled networks, level-k networks, etc). These theoretical classes have been chosen because of concerns about computational tractability, rather than anything to do with the priorities of biological modeling. Unfortunately, little attention has been paid to how likely these networks are from the biological viewpoint. Perhaps the only other unequivocal publication on this topic is that of (M. Arenas, M. Patricio, D. Posada, G. Valiente. 2010. Characterization of phylogenetic networks with NetTest. BMC Bioinformatics 11: 268) More work needs to be done to address this uncertain applicability.

Steven's review appeared in Systematic Biology, which actually has a long tradition of original book reviews that are worth citing in formal research publications. For example, one of the more highly cited papers in the journal is the book review in which Don Colless published his tree-imbalance formula (D.H. Colless. [Review of] Phylogenetics: the Theory and Practice of Phylogenetic Systematics. Systematic Zoology 1982, 31:100-104), which receives continual citation because the formula is still commonly used today. Not everyone publishes original research in their book reviews!

Declaration of potential competing interest: I am currently the Book Review Editor for Systematic Biology, and so I am the one who commissioned Steven's review. However, I take no credit for the contents of the review! The numerous reviewers I have dealt with over the years have produced reviews that varied from excellent through mediocre to ones that needed extensive revision, and on to two that I wrote myself when the original reviewer failed to deliver.

A fundamental limitation of hybridization networks?

In a "hybridization" network, reticulation cycles with three or fewer outgoing arcs are not uniquely defined with respect to trees, clusters or triplets. This point was first noted by Gambette and Huber (2009), although this work will not be formally published until later this year (Gambette and Huber 2012). This seems to be a fundamental mathematical limitation of such networks, which thereby limits what biologists can expect to achieve by performing a network analysis. It is thus a very important point for biologists to understand, as it currently can lead to incorrect interpretation of phylogenetic networks.

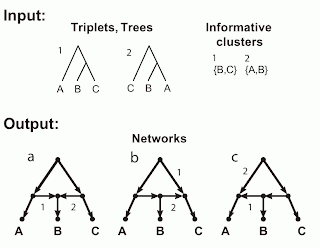
The figure shows two incompatible inputs and the three networks resulting from a hybridization model. The inputs are shown in the figure as trees, triplets and clusters, since in this example these three are identical. There are three taxa (labeled A, B, C), which form two triplets (labeled 1, 2), as shown. (The third possible triplet is not part of this discussion.) Obviously, these triplets also represent two trees, and those trees have two non-trivial clusters.

The figure also shows the three networks (labeled a, b, c) that are encoded (uniquely described) by these triplets / trees / clusters. The relevant arcs of the networks that must be deleted to induce each triplet / tree / cluster are labeled (i.e. deleting edge 1 induces triplet / tree / cluster 1, and similarly for edge 2).

These three networks each have a single reticulation cycle with a single reticulation node (i.e they are level-1 networks) and three outgoing arcs. Note that the three networks differ only in the direction of two of their arcs. Note, also, that the fourth possible combination of these two arcs produces a graph with two roots, which is invalid as a phylogenetic network.

So, these three networks are all associated with the same trees, clusters and triplets. In practice, this means that any one of taxa A, B or C can be attached to the reticulation node. Any network containing such a cycle is not unique – we cannot mathematically distinguish between the three different cycle topologies.

In one sense, this indistinguishability is a mathematically "trivial" ambiguous case. However, this should not make it an under-valued point, because it is likely to have enormous impact on the biological interpretation of networks. After all, every hybridization or horizontal gene transfer potentially creates a reticulation cycle with three outgoing arcs. For example, hybridization between sister taxa will create this situation, although hybridization between non-sister taxa may not (as shown below). When this situation does occur, it will be difficult for us to identify the affected taxa from the network topology alone. This is one fundamental mathematical limitation of using trees (or their subsets such as triplets and clusters) to construct networks.

What is even worse, current computer implementations usually output only one network solution (see Albrecht et al. 2012). If a computer program outputs only a single one of a set of optimal networks, then this may be very misleading. In the case discussed here there are three optimal networks, and biologists might identify the wrong taxon as being the hybrid, depending on which of the three equal networks the program chooses to output. This is an unacceptable situation; and the set of all optimal networks must be produced by each algorithm.

Finally, we may need other (biological) criteria for determining the reticulation taxon. For example, the three networks above represent three different biological scenarios. In scenarios "b" and "c", a daughter taxon apparently hybridizes with its parent taxon, whereas in scenario "a" two daughters hybridize. In other words, temporal order may be deemed to be violated in "b" and "c", thus potentially eliminating them as candidate scenarios. We need, however, to be careful about using this type of argument, as it has not previously been necessary in phylogenetics.

References

Albrecht B., Scornavacca C., Cenci A., Huson D.H. (2012) Fast computation of minimum hybridization networks. Bioinformatics 28: 191-197.

 Gambette P., Huber K.T. (2009) A note on encodings of phylogenetic networks of bounded level. Unpublished ms at: arXiv:0906.4324v1. Tue 23 Jun 2009.

 Gambette P., Huber K.T. (2012) On encodings of phylogenetic networks of bounded level. Journal of Mathematical Biology [in press].

The first phylogenetic network (1755)

Recently, I was asked by Jesper Jansson "where exactly did the first published phylogenetic network appear?" Obviously, the answer to this question can depend on precisely how one defines "phylogenetic", especially as our current understanding of the word did not arise until the late 1800s, notably with the works of St George Jackson Mivart and Ernst Heinrich Haeckel (who actually coined the word "phylogeny"). Nevertheless, if we treat the concept broadly as requiring only an explicit reference to a genealogy, then it seems possible to nominate a candidate.

Mark Ragan suggested to me that, based on his own research as presented in his Biology Direct paper, the most likely candidate is the genealogical network of races of dogs ("Table de L'Ordre des Chiens") produced by Georges-Louis Leclerc, comte de Buffon (1707-1788). I have followed up this lead, and I agree with Mark that it is "not only a network but an explicitly genealogical one". Thus, it seems to me that this publication certainly qualifies as a phylogenetic network. Indeed, even Charles Darwin (from the 4th edition of the Origin, 1866, onwards) acknowledged Buffon as "the first author who in modern times has treated it [evolution] in a scientific spirit".

Buffon's magnum opus was the 36 volumes of the Histoire naturelle générale et particulière (Imprimerie Royale, Paris). The publishing history of this work is a mess, with dozens of French editions and numerous translations, and both official and bootleg printings. Indeed, this was undoubtedly the most popular work on natural history in the late 18th and early 19th centuries. The most readily available printed version today is the one edited by Jean Piveteau in 1954, although various editions are now available online. So, it is important to consult the first edition to arrive at a suitable date.

The illustration shown here is a foldout located between pages 228 and 229 of Volume 5, published in 1755 (Volume 1 had appeared in 1749). A larger GIF version [434 KB] is available for download from my homepage and a PDF version [2.6 MB] is on the RJR Productions webpage. The image is taken from the online (scanned) version of the first edition, located at: http://www.buffon.cnrs.fr/. [It is perhaps worth noting that the first edition of this volume of the Histoire was co-authored by Louis-Jean-Marie Daubenton; but the dog genealogy is clearly Buffon's work alone.]

The Network

On p. 225 of the Histoire, Buffon writes: "Pour donner une idée plus nette de l’ordre des chiens, de leur dégénération dans les différens climats, et du mélange de leurs races, je joins ici une table, ou, si l’on veut, une espèce d’arbre généalogique, où l’on pourra voir d’un coup d’œil toutes ces variétés : cette table est orientée comme les cartes géographiques, et l’on a suivi, autant qu’il étoit possible, la position respective des climats. Le Chien de Berger est la souche de l’arbre : ....." [The 1781 English translation by William Smellie is: "To give a clear idea of the different kinds of dogs, of their degeneration in particular climates, and of the mixture of their races, I have subjoined a table, or genealogical tree, in which all these varieties may be easily distinguished. This tree is drawn in the form of a geographical chart, preserving as much as possible the position of the different climates to which each variety naturally belongs. The shepherd’s dog is the root of the tree ....."]

This text is then followed by a description of the main lines of historical relationship among the dog breeds. Then, on p. 227 Buffon further notes: "Toutes ces races, avec leurs variétés, n’ont été produites que par l’influence du climat, jointe à la douceur de l’abri, à l’effet de la nourriture, et au résultat d’une éducation soignée ; les autres chiens ne sont pas de races pures, et proviennent du mélange de ces premières races : j’ai marqué par des lignes ponctuées, la double origine de ces races métives." [Smellie's translation: "All these races, with their varieties, have been produced by the influence of climate, joined to the effects of shelter, food, and education. The other dogs are not pure races, but have proceeded from commixtures of those already described. I have marked, in the table, by dotted lines, the double origin of these mongrels."]

Buffon's own interpretation of this diagram as a hybridization network thus seems clear enough. If anyone can locate an earlier diagram that can be interpreted as a phylogenetic network, then please let me know.

Update: This later post has more information about Buffon and this network.

Introduction

This blog is about the use of networks in phylogenetic analysis, as a replacement for (or an adjunct to) the usual use of trees. This topic has received considerable attention in the biological literature, not least in microbiology (where horizontal gene transfer is often considered to be rampant) and botany (where hybridization has always been considered to be common). It has also received increasing attention in the computational sciences, although the dialog between the biologists and the mathematicians is not always as clear as it should be.

Networks are acknowledged to have two main uses within phylogenetics: (i) exploratory data analysis, in which conflicting data patterns are visualized and their nature and quantity assessed; and (ii) evolutionary analysis, in which the historical patterns involve not only vertical descent (parent to offspring) but also reticulations due to horizontal processes (such as HGT, hybridization, recombination, and genome fusion).

We are hoping that this blog will help the various groups involved in phyloinformatics focus on a common agenda: the widespread use of networks in phylogenetics. Blog posts might involve news, announcements, new results, commentaries on old results, unpublished (or unpublishable) opinions, or interesting tidbits of information that have no other home. No topic is necessarily excluded.

As always, opinions expressed in this blog are the author's own, and no other blogger necessarily agrees with any of them. We are keen to receive responses to the blog commentaries, and to facilitate discussion of important or interesting topics. We are hoping to have many guest posters, as well. If you would like to contribute to the blog, regularly or even irregularly, then please contact us.