We have had quite a few blog posts about the early metaphors used for genealogical (and other) relationships, whether they be for biology, linguistics or stemmatology. These early metaphors tended to be about trees, either in a literal sense or as a stick diagram of some sort, although we have tried to cover all of the early genealogical networks, as well.
However, this situation does create some potential confusion, because the concept of a genealogical (or phylogentic) tree in the modern world is very much based on the mathematical concept of a tree, which is a graph-theoretical construction. This was clearly not the intention of most of the early authors, especially those writing before Arthur Cayley introduced the mathematical concept (in 1857).
The mathematical version of a tree is a line graph, in which nodes are connected by edges. The edges must be directed if the graph is to represent evolutionary history (ie. the edges point away from the root); and it must be acyclic (or else a descendant could be its own ancestor). The leaf nodes are usually (observed) contemporary taxa, and the internal nodes are (inferred) ancestors. Note that this definition can be applied to both bifurcating trees and to reticulating networks.
This construction is valuable for computational purposes, because we can construct a mathematically optimal tree, which biologists can then use as a starting point for representing the hypothesized genealogy. However, it is not necessarily valuable as a metaphor, which was the purpose of most of the early authors.
There is thus a potential difficulty for modern reads to interpret the older diagrams; and it seems likely, in turn, that the authors of many of the older diagrams would be somewhat befuddled by the modern mathematical restrictions. Sometimes the metaphor and the mathematics will agree, and sometimes they won't.
Branching silhouettes
This issue has been addressed by János Podani in two complementary papers:
- Tree thinking, time and topology: comments on the interpretation of tree diagrams in evolutionary / phylogenetic systematics. Cladistics 29: 315-327 (2013).
- Different from trees, more than metaphors: branching silhouettes — corals, cacti, and the oaks. Systematic Biology 66: 737-753 (2017).
There has long been ambiguity in the use of the term tree in phylogenetic systematics, which is a continuous source of misinterpretation of evolutionary relationships. The basic problem is that while many trees with phylogenetic or evolutionary relevance ... are consistent with graph theory, tree-like visualization of phylogeny may also be done via other types of graphics, especially botanical (or literal) tree drawings. As a consequence, the meaning of such diagrams is not always clear: a given picture may have multiple interpretations in its different parts, and two figures that look similar may actually carry quite different information.Podani resolves the ambiguity by recognizing two fundamental characteristics that any tree diagram will contain: (1) it may show either ancestor-descendant relationships or sister-group relationships; and (2) a time order may be important or it may be disregarded. This leads to a 2x2 representation illustrating the four basic types of "trees" that have been used in phylogenetics.
He gives the four types of branching silhouettes tongue-twisting, but appropriate, names.
The diachronous diagrams are "classic" evolutionary trees with a time dimension, which thus have ancestors as internal nodes and contemporary organisms as the leaves. The achronous diagrams are similar, but they allow descendants to arise from contemporary taxa — they are thus the classic "grade" trees showing morphological advancement, which thus allow paraphyletic ancestral groups. The synchronous diagrams are the modern cladograms, with no observed ancestors (but maybe inferred ones at the internal nodes). The asynchronous diagrams are similar, but they can have ancestors as leaves (eg. "pattern" cladograms of ancestors and descendants together).
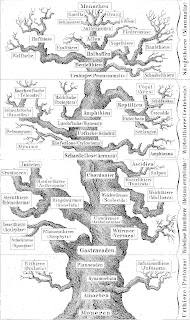
Podani also gives these four branching silhouettes colloquial names. Charles Darwin is often credited with the tree metaphor, but in the Origin of Species he explicitly acknowledges predecessors, although he does not actually name them (see Naudin, Wallace and Darwin — the tree idea). In his own notebooks, his first metaphor is actually a coral (see Charles Darwin's unpublished tree sketches), and this is the name that Podani recommends for the classic evolutionary trees.
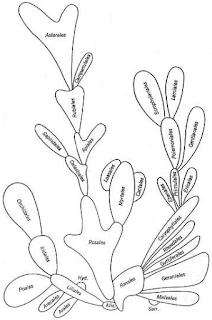
He names the grade trees as cactus, named after the common epithet for the diagram used by Charles Bessey (in 1915) to illustrate plant relationships (see the image below). Furthermore, he recommends oak for the two variants of cladograms, as this is a common epithet for some of the diagrams drawn by Ernst Haeckel (see Who published the first phylogenetic tree?, plus the diagram at the top of this post).
Finally, Podani's work does raise an interesting question. Modern (cladistic) methods of phylogenetics are designed to work with synchronous trees (ie. no observed ancestors). To what extent do these methods work if you try to put fossils into the dataset, which are potential ancestors? After all, this would make the result an asynchronous tree, instead of a synchronous one.


No comments:
Post a Comment