Clades, cladograms, cladistics, and why networks are inevitable

During the work for another post, I stumbled on a kind of gap-in-knowledge that has nagged me for quite some time. This gap exists because researchers like to stay within chosen philosophical viewpoints, rather than reassessing their stance.

This gap involves the use of cladistic methodology in a manner that obscures information about evolutionary history, rather than revealing it. A clade, a subtree in a rooted tree that fulfills the parsimony criterion (or, indeed, any other criterion), may or may not reflect monophyly in a Hennigian sense, i.e. inclusive common origin. This is especially true for studies of extinct lineages.

I will explore this idea here in some detail.

Assumptions when studying fossils

Phylogenetic papers dealing with the evolution of extinct groups of organisms frequently use strict consensus trees (typically cladograms) of a sample of equally parsimonious trees (MPT) as the sole or main basis for their conclusions. They do this under two important implicit assumptions:

• The morphological differentiation patterns encoded in a character matrix provide a generally treelike signal. In other words, the data patterns in the morphological matrix can be explained by a single, dichotomous, 1-dimensional graph. This assumption is also the basis for posterior filtering or down-weighting of characters that support splits (taxon bipartitions) conflicting with the branches in the inferred tree(s).
• Morphological evolution is generally parsimonious. Although this may apply for characters that evolved only once or only evolve under very rare conditions, total evidence and DNA-constrained analysis demonstrate that this is not generally the case: the tree inferred by total-evidence or molecular constraints is typically longer than the tree(s) with the fewest character changes inferred on the morphological partition alone.

Another implicit assumption seems to be that all fossil specimens must represent extinct sister clades, and that no fossil specimen is ancestral to any other (or to an extant species) — hence, all taxa can be treated as terminals (not ancestors). Rooting typically relies on outgroups, under the assumption that ingroup-outgroup branching artefacts (such as long-branch attraction) play no role for parsimony inference when using morphological data sets.

In many of these morphology-phylogenetic papers (using parsimony or other methods) the authors state that they have conduct a “cladistic” study (I also made this error in my masters thesis; Grimm 1999). Cladistics is a classification system established by Hennig (1950) that relies on synapomorphies, exclusively shared, derived traits, that are linked with groups of inclusive common origin, the so-called monophyla.

Over 90 years earlier, Haeckel (1866) used the German word monophyletisch to refer to “natural” groups defined by a shared evolutionary history (a common origin). The latter could also include what Hennig identified as paraphyla: groups that have a common origin, but are not inclusive. To avoid confusion between Haeckelian and Hennigian monophyletic groups, Ashlock (1971) suggested the term holophyletic for the latter. This can be useful when a classification should recognise evolutionary relationships but needs to classify potentially or definitely paraphyletic groups for reasons of practicality (see e.g. Bomfleur, Grimm & McLoughlin 2017). Here, I will stick to Hennig’s terminology, as it is much more commonly used (although not necessarily correctly applied).
 
Hennig’s monophyla are from a theoretical (and computational) point of view a brilliant concept, as they can be inferred using a rooted tree. The test for monophyly is simple: Do A and B have a common ancestor? If yes, identify all taxa that are part of the same subtree as A and B. Unfortunately, we often find more than one possible tree, and roots can be misleading.

Strict consensus trees poorly represent the alternative topologies in a MPT sample

All consensus-tree approaches are limited to depicting the topological alternatives in a tree sample, but strict consensus trees are probably the worst (see e.g. Felsenstein 2004, chapter 30). They also have become obsolete with the development of consensus networks (Holland & Moulton 2003), and their subsequent implementation in freely accessible software packages such as SplitsTree (Huson 1998; Huson & Bryant 2006) and, more recently, the PHANGORN library for R (Schliep 2011; Schliep et al. 2017).

Figure 1 illustrates this difference for two extreme cases of binary matrices and their MPT collections. The two datasets in Fig. 1 reflect a substantially different data situation. The data in one matrix are perfectly tree-unlike (completely “confused about relationships”): any possible non-trivial bipartition of the 5-taxon set is supported by one (parsimony-informative) character. The data in the other matrix reflect two incongruent trees: each character is compatible with either one of the trees (parsimony-informative characters) or both trees (unique characters). The non-treelike matrix allows for many more MPTs than does the tree-like matrix, which results in two MPTs perfectly matching the two conflicting true trees. But both consensus analyses result in the same, unresolved (polytomous) strict consensus tree. In contrast, the two consensus networks highlight the difference in the quality between the data sets and the MPT sample.

Fig. 1 Non-treelike and treelike data, and the representation of their most-parsimonious tree collections as strict consensus trees and networks

Another example is shown in Figure 2, which shows four trees that differ only in the placement of one taxon (T8). This is a common phenomenom, particularly when dealing with extinct groups of organisms. The three main reasons for such topological ambiguity are:

1. Indicisive data regarding the exact position of T8 with respect to the members of the red (T1–T4) and green clades (T5–T7).
2. Conflicting data, T8 shows a combination of traits that are otherwise restricted to (parts of) the green or red clade.
3. T8 is an ancestor or primitive member of the green or red clade, or both. 

Fig. 2 A single rogue taxon (T8) with ambiguous affinities collapses the strict consensus tree. In contrast, the conensus network can simultaenously show all alternatives, and identifies T8 as the source of topological ambiguity.

The strict consensus tree shows only three clades (three pairs of sister taxa) and a large polytomy, but the strict consensus network shows simultaneously the topology of all four trees and the position of T8 in these trees. From the consensus network, it is clear that the members of the red and green clades share a common origin. T8 can easily be identified as the rogue taxon (lineage).

Cladograms are incomplete representations of evolutionary trees

Figure 3 shows one of the first phylogenetic trees ever produced, and how it would look in the results section of a cladistic study. The tree was produced 150 years ago by Franz Martin Hilgendorf — more than 100 years before Hennig’s ideas were introduced to the Anglo-Saxon world and became mainstream. Hilgendorf was a palaeontology Ph.D. student at the same institute (in Tübingen, Germany) that also promoted me. Quenstedt, his supervisor, forced a quick promotion to get him and his heretic Darwinian ideas out of his university; there are thus no figures in Hilgendorf's thesis, and he published a phylogenetic tree only after he left Tübingen. It shows the evolution of derived forms (terminals) from putative ancestral forms (placed at the nodes) of fossils snails from the Steinheimer Becken, and clearly distinguishes ancestors and sisters. At some point, Hilgendorf even considered including the reticulation of lineages to better explain some forms, but later dropped this idea, feeling it would violate Darwin’s principle (Rasser 2006; see The dilemma of evolutionary networks and Darwinian trees).

Fig. 3 Hilgendorf's phylogenetic tree of fossil snails and its representation in form of a cladogram. The coloured fields and boxes refer to a series of nested clades, which here equal monophyletic groups.

Translating Hilgendorf’s tree into a cladogram comes with a loss of information about the evolution of the snails. Some ancestors are placed as sisters to their descendants (e.g. 18 vs. 18a and 19) and others are collected in a polytomy together with their descendants/descending lineages (e.g. 15, the ancestor of the siblings 16, 17, and the 18+). The loss of information regarding assumed ancestor-descendant relationships is dramatic. But this is no problem for cladistic classification: all clades in the cladogram in Fig. 3 (boxes) refer to Hennigian monophyletic groups seen in the original phylogenetic tree (coloured backgrounds). The polytomies in the cladogram are hard polytomies and do not reflect uncertainty or ambiguity. This contrasts with most cladograms depicted in the phylogenetic (“cladistic”) literature, where polytomies can also reflect lack of support or topological ambiguity.

Accepting the possibility that some fossils (fossil forms) may be ancestral to others (or their modern counterparts), or at least represent an ancestral, underived form, we actually should not infer plain parsimony trees but median networks (Bandelt et al. 1995). Median networks and related inferences (reduced median networks: Bandelt et al. 1995; median joining networks: Bandelt, Forster & Röhl 1999) work under the same optimality criterion (evolution is parsimonious) but allow taxa to be placed at the nodes (the “median”) of the graph. In doing so, they depict ancestor-descendant relationships. That they have not been used for morphological data so far, nor in palaeophylogenetic studies (as far as I know), may have to do with their vulnerability to homoplasy and missing data. High levels of homoplasy are common in morphological matrices, and missing data can be a problem when working with extinct organisms.

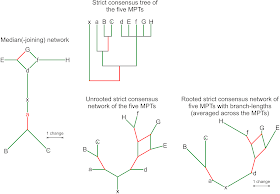
An ideal matrix, in which each divergence is followed by the accumulation of synapomorphies (or “autapomorphies”, unique traits, close to the tips), results in a median network perfectly depicting the evolutionary tree (Figure 4). As soon as convergent evolution steps in, a median network can easily become chaotic, although less so for a median-joining network. Note that half of the characters are homoplasious, and yet the median-joining network is still largely treelike (Fig. 4), with only one 2-dimensional box. The true tree is included in the network; but an E-G clade evolving from D is indicated as alternative to the correct (and monophyletic) FGH clade, with G and H evolving from F. Another deviation from the true tree is that A, the ancestor of B and C, is not placed at the node, but is closer to the all-common ancestor X.

Fig. 4 Two datasets, one without (left) and one with homoplasy (right), and their median(-joining) networks. Green branches refer to exact fits with the true tree, red indicate deviation or conflict with the true tree.

Paraphyletic clades...

Figures 5A and B show the corresponding MPT for the ideal matrix and the strict consensus tree vs. strict consensus network for the matrix affected by homoplasy. As our ideal matrix includes actual ancestors, the MPT rooted with the most primitive taxon X (the common ancestor of A–H) cannot resolve the exact relationships, in contrast to the median network. It thus represents the true tree only partly. But it also does not show any clade that is not monophyletic.

In the case of the partly homoplasious data, the median-joining network reconstructs a synapomorphy of the clade BC, because A is not placed on the node. This is because one character in our matrix is a methodologically undetectable parallelism — the same trait evolved in the sister taxa B and C, but only after both evolved from A. Clade BC is non-inclusive (paraphyletic), since A is the direct ancestor of both B and C and the clade BC lacks a real synapomorphy (if we go back to Hennig's concept). The reconstructed A would, however, be a stem taxon and clade BC would be inclusive (monophyletic) with one (inferred) synapomorphy. But this is a purely semantic problem of cladistics. In the real world, we will hardly have the data to discern whether A represents: the last common ancestor of B and C, a stem taxon of the ABC-lineage (a’), a very early precursor of B or C (b/c), or an ancient sister lineage of A, B, and/or C (a*). For practicality, one would eventually include all fossil forms with A-ish appearance in a paraphyletic taxon A (Fig. 5C), in (silent) violation of cladistic classification, to name only monophyletic groups.

Fig. 5A The median network compared to the single most-parsimonious tree inferred based on the ideal matrix

Fig. 5B The median-joining network compared to the strict consensus tree and networks of five most-parsimonious trees inferred based on the matrix with homoplasy. Red edges indicate deviations from or conflicts with the true tree.

Fig. 5C Potential monophyla that could be inferred from the median-joining network (Clades XY), when rooted with the most ancient taxon X. Groups that are monophyletic according to the true tree in blue, groups that are not in orange.

The strict consensus tree of the five MPTs that can be inferred from the homoplasious matrix shows only the paraphyletic (pseudo-monophyletic) clade BC and two monophyletic clades (ABC and D–H); and it contains no further information about the actual topology of the five MPTs. Its lack of resolution is due to the ancestors, which have typically less derived traits (no autapomorphies and fewer synapomorphies), in combination with the homoplasy-induced topological ambiguity. In contrast, the strict consensus networks reveal that all five MPTs place D, the ancestor of the D–H lineage, as (zero branch length) sister to a technically paraphyletic E–H clade, thereby identifying D as the most primitive form of the monophyletic D–H clade. Furthermore, all MPTs recognise a paraphyletic FH clade (F again a zero-length branch). They disagree in the placement of G, which is either sister to F+H (monophyletic FGH clade) or sister to E (a wrong EG clade).

... and monophyletic grades

Figure 6 shows a scenario in which paraphyletic groups are resolved as clades and monophyletic groups form grades, both because of outgroup-ingroup branching artefacts. The derived outgroup O is notably distinct from all ingroup taxa showing a character suite of convergently evolved traits that are randomly shared with parts of the ingroup. Within the ingroup, members of clade DEF are much more derived than are A and C.

Fig. 6 Ingroup-outgroup long-branch attraction can turn monophyla into grades and paraphyla into clades. The ingroup (A–F) consists of a sequence of nested monophyletic lineages (green shades) including two taxa (lowercase letters) that are ancestral to others. Each ingroup lineage evolved (convergent) traits also found in the outgroup O. The data allow inferring two MPTs that misplace O. The outgroup-misinformed root leads to a series of nested clades that a paraphyletic. Splits congruent with the actual monophyletic groups in green, those in conflict with the true tree in red.

Parsimony-tree inference finds two MPTs, which, rooted with the outgroup O, recognise a distinctly paraphyletic A–D+X clade. In both outgroup-rooted MPTs, the monophyletic DEF group is dissolved into a grade. By the way: using neighbour-joining (NJ) to find a tree fulfilling the least-squares (LS) criterion based on the corresponding pairwise mean distance matrix, the outgroup-inferred root is still misplaced with respect to the primitive taxa (X, A–C), but the DEF monophylum is correctly resolved as a clade. Call the Spanish Inquisition! A “phenetic” clustering algorithm finds a tree that is less wrong than the MPTs.

The most comprehensive display of the misleading signal in this matrix is nevertheless the neighbour-net (NNet; Figure 7), which includes both the parsimony and LS-solutions, and it can be used to map the competing support patterns surfacing in a bootstrap analysis of the data. In this network we can see that the signal is not compatible with a single tree, and that the signal from the distant outgroup O is too ambiguous for rooting the ingroup. Based on this graph, one can argue to delete the outgroup, thereby deleting all non-treelike signal — a NNet (or median network) excluding O matches exactly the true tree.

Fig. 7 Neighbour-net based on mean pairwise distances (same data in Fig. 6). The outgroup O provides a strongly ambiguous (non-treelike) signal, thus, triggering a series of splits (in red) conflicting the true tree (shown in grey). Edges compatible with the true tree shown in green. The numbers refer to non-parametric bootstrap support estimated under three optimality criteria: least-squares (LS; via neighbour-joinging), maximum likelihood (ML; using Lewis' 1-parameter Mk model), and maximum parsimony (MP) and 10,000 (pseudo)replicates each. Upper right: A splits-rose illustrating the competing support patterns for proximal splits involving O: green — split seen in the true tree, reddish — the competing splits seen in the two MPTs.

We need to accept that a clade, a subtree in a rooted tree (see e.g. Felsenstein 2004) fulfilling the parsimony criterion (or any other criterion), may or may not reflect monophyly in a Hennigian sense, i.e. inclusive common origin. Thus, it is imperative to distinguish between a classification concept that interprets trees (cladistics) and the method used to infer trees (typically parsimony, in the case of extinct lineages). This is especially so when one has to work with stand-alone data, such as morphological data of extinct groups of organisms.

Aside from the clades/grades ↔ monophyla / paraphyla / can't-say problem, the instability of clades in a parsimony or otherwise optimised rooted tree, or the alternative clades that can be inferred from the more data-comprehensive networks, make it difficult to enforce a strictly cladistic naming scheme. For the example shown in Fig. 2, we would be unable to name the red and green clades until the exact position of T8 is settled (see also Bomfleur, Grimm & McLoughlin 2017). In the end, the overall diversity patterns (studied using exploratory data analysis) may remain the most solid ground for classification.

It should also be obligatory in phylogenetic studies to use networks to display both competing topological alternatives and incompatible data patterns. There should also always be some information on edge-lengths. Consensus trees are insufficient, as they mask conflicting data patterns, and cladograms mask the amount of change.

References

Ashlock PD. (1971) Monophyly and associated terms. Systematic Zoology 20:63–69.

Bandelt H-J, Forster P, Röhl A. (1999) Median-joining networks for inferring intraspecific phylogenies. Molecular Biology and Evolution 16:37-48.

Bandelt H-J, Forster P, Sykes BC, Richards MB. (1995) Mitochondrial portraits of human populations using median networks. Genetics 141:743-753.

Bomfleur B, Grimm GW, McLoughlin S. (2017) Figure 8 of: The fossil Osmundales (Royal Ferns)—a phylogenetic network analysis, revised taxonomy, and evolutionary classification of anatomically preserved trunks and rhizomes. PeerJ 5:e3433.

Felsenstein J. (2004) Inferring phylogenies. Sunderland, MA, U.S.A.: Sinauer Associates Inc.

Grimm GW. (1999) Phylogenie der Cycadales. Diploma thesis. Eberhard Karls Universität. [in German]

Haeckel E. (1866) Generelle Morphologie der Organismen. Berlin: Georg Reiner.

Hennig W. (1950) Grundzüge einer Theorie der phylogenetischen Systematik. Berlin: Dt. Zentralverlag.

Holland B, Moulton V. (2003) Consensus networks: A method for visualising incompatibilities in collections of trees. In: Benson G, and Page R, eds. Algorithms in Bioinformatics: Third International Workshop, WABI, Budapest, Hungary Proceedings. Berlin, Heidelberg, Stuttgart: Springer Verlag, p. 165–176.

Huson DH. (1998) SplitsTree: analyzing and visualizing evolutionary data. Bioinformatics 14:68–73.

Huson DH, Bryant D. (2006) Application of phylogenetic networks in evolutionary studies. Molecular Biology and Evolution 23:254–267.

Rasser MW. (2006) 140 Jahre Steinheimer Schnecken-Stammbaum: der älteste fossile Stammbaum aus heutiger Sicht. Online version, originally published in Geologica et Palaeontologica, vol. 40.

Schliep K, Potts AJ, Morrison DA, Grimm GW. (2017) Intertwining phylogenetic trees and networks. Methods in Ecology and Evolution DOI:10.1111/2041-210X.12760.

Schliep KP. (2011) Phangorn: phylogenetic analysis in R. Bioinformatics 27:592–593.