A fundamental limitation of hybridization networks?

In a "hybridization" network, reticulation cycles with three or fewer outgoing arcs are not uniquely defined with respect to trees, clusters or triplets. This point was first noted by Gambette and Huber (2009), although this work will not be formally published until later this year (Gambette and Huber 2012). This seems to be a fundamental mathematical limitation of such networks, which thereby limits what biologists can expect to achieve by performing a network analysis. It is thus a very important point for biologists to understand, as it currently can lead to incorrect interpretation of phylogenetic networks.

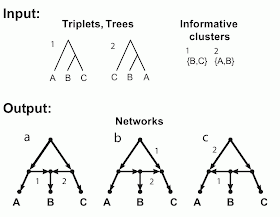
The figure shows two incompatible inputs and the three networks resulting from a hybridization model. The inputs are shown in the figure as trees, triplets and clusters, since in this example these three are identical. There are three taxa (labeled A, B, C), which form two triplets (labeled 1, 2), as shown. (The third possible triplet is not part of this discussion.) Obviously, these triplets also represent two trees, and those trees have two non-trivial clusters.

The figure also shows the three networks (labeled a, b, c) that are encoded (uniquely described) by these triplets / trees / clusters. The relevant arcs of the networks that must be deleted to induce each triplet / tree / cluster are labeled (i.e. deleting edge 1 induces triplet / tree / cluster 1, and similarly for edge 2).

These three networks each have a single reticulation cycle with a single reticulation node (i.e they are level-1 networks) and three outgoing arcs. Note that the three networks differ only in the direction of two of their arcs. Note, also, that the fourth possible combination of these two arcs produces a graph with two roots, which is invalid as a phylogenetic network.

So, these three networks are all associated with the same trees, clusters and triplets. In practice, this means that any one of taxa A, B or C can be attached to the reticulation node. Any network containing such a cycle is not unique – we cannot mathematically distinguish between the three different cycle topologies.

In one sense, this indistinguishability is a mathematically "trivial" ambiguous case. However, this should not make it an under-valued point, because it is likely to have enormous impact on the biological interpretation of networks. After all, every hybridization or horizontal gene transfer potentially creates a reticulation cycle with three outgoing arcs. For example, hybridization between sister taxa will create this situation, although hybridization between non-sister taxa may not (as shown below). When this situation does occur, it will be difficult for us to identify the affected taxa from the network topology alone. This is one fundamental mathematical limitation of using trees (or their subsets such as triplets and clusters) to construct networks.

What is even worse, current computer implementations usually output only one network solution (see Albrecht et al. 2012). If a computer program outputs only a single one of a set of optimal networks, then this may be very misleading. In the case discussed here there are three optimal networks, and biologists might identify the wrong taxon as being the hybrid, depending on which of the three equal networks the program chooses to output. This is an unacceptable situation; and the set of all optimal networks must be produced by each algorithm.

Finally, we may need other (biological) criteria for determining the reticulation taxon. For example, the three networks above represent three different biological scenarios. In scenarios "b" and "c", a daughter taxon apparently hybridizes with its parent taxon, whereas in scenario "a" two daughters hybridize. In other words, temporal order may be deemed to be violated in "b" and "c", thus potentially eliminating them as candidate scenarios. We need, however, to be careful about using this type of argument, as it has not previously been necessary in phylogenetics.

References

Albrecht B., Scornavacca C., Cenci A., Huson D.H. (2012) Fast computation of minimum hybridization networks. Bioinformatics 28: 191-197.

Gambette P., Huber K.T. (2009) A note on encodings of phylogenetic networks of bounded level. Unpublished ms at: arXiv:0906.4324v1. Tue 23 Jun 2009.

Gambette P., Huber K.T. (2012) On encodings of phylogenetic networks of bounded level. Journal of Mathematical Biology [in press].